Accurate field measurements at Bracciano,
Italy reveal a significant anomaly “down the hill”
versus “across the hill”, consistent with projection of
that entire crop picture from the sky above, by the
shortest possible path to the ground below
Because the new crop picture at Bracciano, Italy on May
20, 2012 appeared along the side of a steep hill, it
became of some interest to measure its exact dimensions
in the field. These are now shown below, for both its
large outer circle and its small inner circle:

Each circle is slightly smaller when measured
carefully on the ground, going “down the hill” versus
“across the hill”. Its large outer circle measures 54.15
versus 55.10 meters in each direction respectively,
while its small inner circle measures 15.60 versus 16.20
meters. Right away we can rule out any possible
construction of this crop formation by local human
hoaxers, unless they were clumsy enough to make a
“one meter error” using rope and boards, away from a
perfect circular shape!
Next we can estimate the absolute slope of that hill,
relative to the Earth’s surface, by measuring from a
photograph which includes both the crop picture and also
the distant horizon:

Several “horizon” photographs were tested in this way,
and all yielded a slope of 10o to 11o.
Can the slope of a local field influence the precise
dimensions of any crop picture which appears within it?
This problem was discussed as long ago as 1999 by Jack
Sullivan, who wrote: “Some crop circles have appeared on
hillsides or other sloping ground. There have also been
reports from eyewitnesses, to suggest that the energy
which creates authentic crop circles may be projected
down towards the Earth from an unknown source
located above. In fact, many of those hillside circles,
when measured carefully on the ground, turn out to be
projected ellipses” (adapted from
Crop Circles An Elliptical View).
Concerning our new example at Bracciano. Italy in May of
2012, one might imagine that the steep slope of 10o
to 11o found for that hill, where the crop
picture appeared, might change its precise shape by the
amount measured: say to 54.15 meters “down the hill”
versus an unaltered 55.10 meters “across the hill”? We
can reconstruct a hypothetical geometry which might
produce those results as follows:
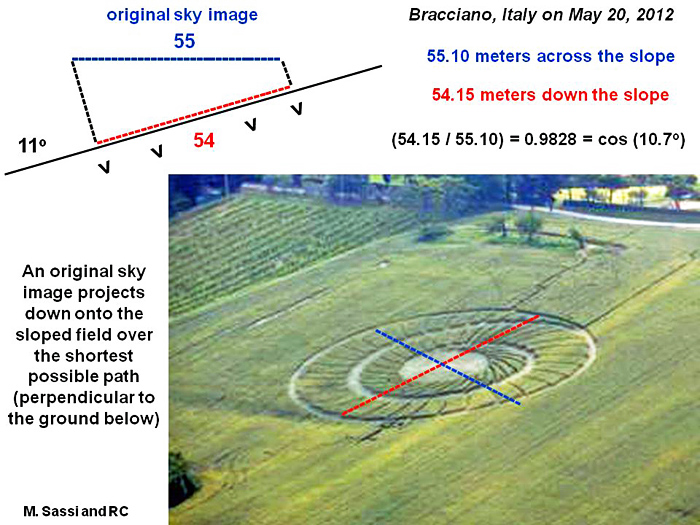
Starting from an original “sky image” of diameter 55.10
meters, the simple act of projection down onto a steep
hill gives the correct slope of 10.7o, close
to 10o or 11o as measured relative
to a distant horizon.
There are two possible ways by which a “sky image” might
project down onto a steep hill. In the case shown, that
“sky image” seems to project by the shortest possible
path to the ground below. Thus the “downhill” field
image becomes slightly shorter than the original image,
as 54 and not 55 meters. Alternatively, one could
imagine another scenario where the “sky image” projects
by the longest possible path to the ground below. Then
the “downhill” field image would become slightly longer
than the original image, as 56 and not 55 meters. We
cannot say which kind of projection might be found by
careful measurement of other crop pictures, yet a
“shortest path” seems to have been followed here.
A small inner circle at Bracciano yields similar
results, although the accuracy of measurement may not be
quite as great, owing to its reduced size:
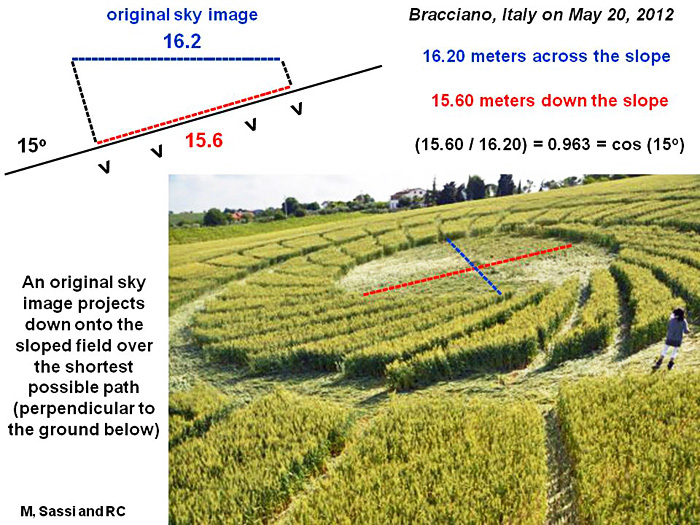
For that small inner circle, we can calculate a downhill
slope of 15o based on the shortest possible
path of projection, while the true value of slope is 10o
to 11o.
Further careful measurements such as these, for other
crop pictures in the summer of 2012, when they appear on
steep hillsides, may help to illuminate the exact
mechanisms by which paranormal field images are created.
In any case, the present data seem to argue against
possible human construction of Bracciano, Italy using
“rope and boards”, because that simple method can only
produce perfect circles, and not complex hillside
ellipses. Although
nothing is impossible, and other more sophisticated
techniques might be capable of doing so.
Marina Sassi and Red Collie (Dr. Horace R. Drew) with
help from Julia Flafh