Manton Drove, nr Marlborough, Wiltshire. Reported 2nd June.

Map Ref: SU169676

This Page has been accessed
Hit Counter
Updated  Monday 21st October 2013

  
AERIAL SHOTS GROUND SHOTS DIAGRAMS FIELD REPORTS COMMENTS ARTICLES
03/06/12 03/06/12 21/10/13 04/06/12 27/06/12 03/06/12

Image Simone Watts Copyright 2012

Reconstruction of the
2012 Manton Drove formation

By Zef Damen

Images Sonya Bailey Copyright 2012

 

Image Jay Goldner Copyright 2012

Diagrams www.maya48.com Copyright 2012

Diagrams Johan Andersson  Copyright 2012

 

Diagram Bertold Zugelder Copyright 2012

Diagram Nyako Nakar Copyright 2012

This geometry study is a continuation of the analysis of the Manton Drove Crop Circle. While this study does not offer new insight for the polar clock's date/time, the design maintains focus on the role of Pi in this crop circle geometry.

This geometry promotes the theory that a squared circle can be proven if these dimensions are reflected in two adjoining sides of a geometric object: 1/2 the square root of Pi and 1/2 the square root of 2. The inscribed tan quadrilateral, named "Karotumus" (for its tasty discovery; accent on the second syllable), appears to include these dimensions. Intuitively, the 1000-units-diameter blue corral (the circle) should limit the infinity of Pi, but does it? .... or is this the "Enigma of Karotumus"?


(Focus on the circle squaring properties of the right triangle within Karotumus: angles = 62.402.., 27.597.., 90 degrees.)
 
This new concept of Pi will intrigue geometers as well as crop circle aficionados. Please add the following comment after the sentence "Focus on the circle squaring properties ...": 
 
Consider also that the Pythagorean Theorem confirms these angles:
 
(1/2 square root of Pi = 0.88622692545275801364908374167057...)
 
a = 463.25137517610424292137983379471... (top horizontal side)
b = 886.22692545275801364908374167057...  (left vertical side)
c = 1000 units (hypotenuse; radius of large magenta circle)
 
a˛ + b˛ = c˛ = 999999.99999999999999999999999999...

Here's the latest research on the Manton Drove crop circle's geometry as it relates to the Barbury Castle's Pi crop circle (June, 2008).

I was curious about the rounding of Pi (from 3.1415926535... to 3.141592654...) in the Pi crop circle since I believed that a number is not rounded if an ellipsis is used to continue that number. But Bert Janssen's conjecture on those "three little circles" in the Pi crop circle provided great insight: that ellipsis may also convey circle squaring information! (see: www.cropcirclesandmore.com ) 

Interestingly,  the circle makers clearly demonstrate their geometry expertise by choosing this tenth digit of Pi: not only does this tenth digit (3) properly round to 4, but the relative diameters of the "three little circles" (the ellipsis) within that 36-degree angle appear to equal  4/3/2. 

Today, preliminary "reverse engineering" of the Barbury Castle's Pi crop circle's "three little circles" around the circle-squaring 62.403.. degree angle (from the Karotumus research) produces a fascinating correlation: the tangent between the two smaller circles is very close to the 62.403.. degree angle! (see above BCPi image). 

Perhaps, this Pi crop circle's subtle clue for squaring a circle might soon be confirmed and be followed by a geometric solution for proving the square (via the non-isosceles right triangle which includes the 62.403.. angle). 

A great day for triangular Pi !
 

Note:  The 4/3/2 relative diameters are actually the three circles' tangent-to-tangent chord lengths.

This Symmetry design, further exploration of the Manton Drove crop circle, appears to provide important clues for "squaring the circle". Focus on the two large, green, scalene triangles and consider the diameters of the small circles, especially when these circles are analyzed in groups of two (one small + one slightly larger). But the horizontal centre (not shown) of the green parallelogram may contain the more important clue.


To celebrate the final day of the 13th baktun (o oo oo o o oo), here's a design that colourfully articulates the significant lines in a squared circle.
 
Humour: When asked to summarize his articulation of the geometry of a squared circle, Pythagoras just winked and blurted "My Pi, My Pi".

To celebrate the beginning of the 14th baktun, here's a design that colourfully articulates the symmetry of a squared circle. This design, rich with "new era" symbolism, proffers that circles and their squares have impressive alignment with universe significance. The full lengths of the light blue lines on this 2000-units-diameter circle are equal to the square root of  2 * 1000  (= 1414.2135623730950488016887242097...). 

A personal interpretation of this new era symbolism: 

"What is important in life is not what you can do or have done, but always what you believe that you can do ... for your life's work often complements what you believe." 

The squared circle symbolizes that which is believed to be impossible and the snowflake symbolizes the uniqueness of every human being. The design is coloured to emphasize the inscribed parallelogram, that both squares the circle and symbolizes the unseen, parallel spiritual realities of our material universe.

 

A 14th baktun, first day perspective on the challenge of squared circles. This design symbolizes the expected discovery of a solution to this Greek challenge during the next 143999 days of the 14th baktun.

"In 2013 we taste the cheese, moving closer."

These two squared circles (light blue; the larger created first) display the essence of squared circle geometry and suggest that only three points are required to square the circle. In the large, green scalene triangle, the left diagonal line (essence of a square) and the bottom horizontal line (essence of a circle) reveal the square roots of 2 and of Pi, respectively. Does this design display the elusive and transcendent geometric associations that prove the circle's square? (large circle's diameter = 2000 units; smaller circle's radius = 1/2 square root of 2 * 1000)

 
Interestingly, this design's geometry appears to confirm a thesis about proving the square of a circle: 

When half of the side length of the larger square (1/2 the square root  of Pi) equals half of the diagonal length of the smaller square (1/2 the square root of Pi), both circles are squared. This equal condition exists only when both circles are correctly squared. And Pi does not constrain this geometric proof of a squared circle since both line lengths are equal, despite the number of decimal digits in Pi ... if the thesis is correct. 

Zdenka Pávková's June 2012 analysis of the Manton Drove crop circle reinforced my belief that one side of a circle's inscribed square would be required to "anchor" a geometric proof. The smaller light blue circle in this design successfully incorporates one side of an inscribed square (full square not displayed).

 

The precision of this circle squaring method is directly related to the exact length of the left diagonal side of the scalene triangle (this side represents the square root of 2) and to the intersection of a point on the circle's circumference with a point on the length of the golden "T" pin (this side represents the square root of Pi). This squaring method begins with the golden circle, then a chord (one side of an inscribed square), then the "T" pin that effectively creates the scalene triangle. 

Interestingly, the other two squared circles seem to be clues to geometrically proving the square of the golden circle: each diagonal side of the green scalene triangle effectively squares a circle when the other side of the triangle is the diameter of that circle. 

The small red circle helps create the symbolism of an exclamation mark, the red triangle an allusion to trigonometry that also squares this circle.

Correction: The "T" pin concept as presented in the recent design is not correct - the scalene triangle cannot be created this way. "Close, but no cigar!" (of US origin from the mid-20th century when fairground stalls gave cigars as prizes). But research still shows that the scalene triangle - when drawn precisely - squares the circle and its diagonal sides facilitate the drawing/squaring of two additional circles.

 

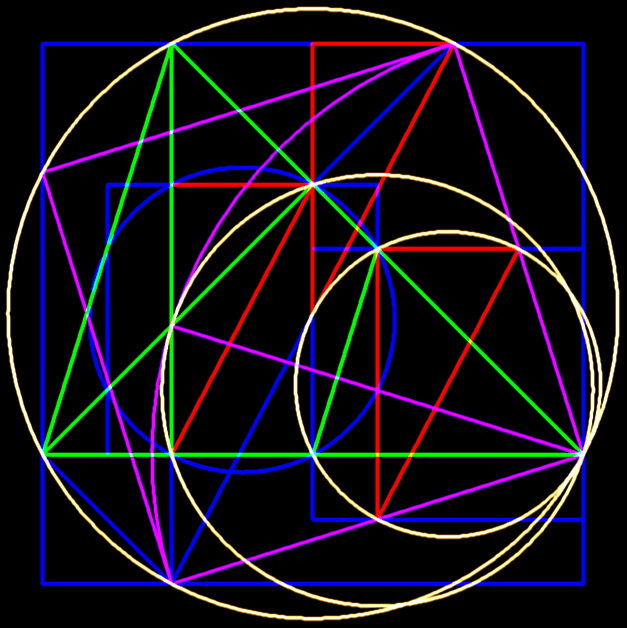
Presenting the essential scalene triangle of squared circle geometry, suggesting that only three points are required to square the circle:
 
Given:
- pivot point is at the top left of the diagram.
- golden circle (diameter = 2,000,000 units) is given.
- green line at 45 degrees (length unknown) is given.
- horizontal line at 0 degrees (pivot line, length unknown) is given.
- shortest side of the scalene triangle = side of an inscribed square.
- light blue arc is a portion of a circle (radius = golden circle's chord).
- dark blue arc is a portion of a circle (radius = golden circle's
diameter).
 
Method:
- rotate golden circle and its chord counter clockwise to create scalene triangle.
- many lines shown cannot be drawn until the rotation is stopped.
- knowing when to stop the rotation is the challenge!
 
Comments: 

The dark blue arc (circle's diameter = 4 mil. units) is the "pivotal" arc (the more important geometric association with the pivot point at the top left of the diagram) because the large, dark blue, Pythagorean triangle confirms the "square of the circle": the golden circle (diameter = 2 mil. units) is squared by the small red Pythagorean triangle at the top of the diagram. 

Thus both circles, golden and dark blue, are squared by the same Pythagorean triangle (same angles): the area of the square of the dark blue circle is exactly four times the area of the square of the golden circle. And the golden "I" highlights two equal line lengths: length of square's diagonal (midpoint to midpoint) = length separating the circle's two chords (midpoint to midpoint).

This Scalene Progression design finalizes this study and commemorates Pi Day 2013 (now 10 trillion digits of Pi).

The design reveals that only 3 points are required to "square the circle" (left side of green triangle and of horizontal side reflect the square roots of 2 and of Pi; large circle's diameter = 1 million units). The diameters are decremented by half the square root of 2: lengths from largest to smallest = 1000000.0, 707106.781, 500000.0.

The red triangle provides a new "no Pi" trigonometry formula for the area of the circle. With a right triangle having an hypotenuse as the radius of a circle and the cosine angle (near the circle's center) = 27.597112635690604451732204752339.. degrees, the trigonometry formula becomes:

Area = ((cos 27.597112635690604451732204752339.. ) x diameter) squared

Discussion:

That this cosine angle might complement Pi digit-for-digit in a perfectly squared circle ... and that this Pythagorean triangle exists in every squared circle ... hints that Pi Day has always had a certain Pythagorean ambience. Perhaps, Pythagoras even contemplated this right triangle's always-present, geometric sibling: a circle-squaring scalene triangle. The lines in this Scalene Progression design directly or effectively square the four circles.

This geometry and the supporting trigonometry hint that squaring the circle may be less "impossible" than finding the limit of Pi digits. After all, the three points of a certain scalene triangle seem to be a sufficient number on a circle to determine its square (although 8 would be the maximum required since a circle's square rests upon 8 points ... only).

Which leads us to this Pi Day perspective: Some Pi are square, some are round, but no Pi is triangular.

Update 21/10/2013

I-Square method

The I-Square method* is derived from analysis that a squared circle has only 8 points of contact between the circle and its square (plus later conjecture that a solution to "squaring the circle" requires geometric association of the square root of Pi and the square root of 2). Completing the square requires a few more steps; complete the inscribed square for better display of the geometry. 

 
Squaring the circle with a protractor and compass (I-Square method):
 
1. Draw a 45-degree angle with the sides at 135 and 180 degrees.
2. Draw a center line at 152.4 degrees** from the vertex of the angle.
3. Mark the length of the circle's radius along the centre line from the vertex.
4. Draw the circle with the compass point at the left end of the radius. 

The two sides of the 45-degree angle and the vertex identify 3 points of the circle's square and creates a chord that has length equal to the side length of the circle's square. 

This is not a solution to the Greek challenge of "squaring the circle" but reveals the unique scalene triangle that might help prove that the circle is squared. Another straight line drawn between the two points, one on each side of the angle, creates a diagonal chord that has length equal to the side length of a square inscribed in the circle. 

* "I-Square" is a nickname referring to "Impossible Square" which alludes to popular belief that a circle cannot be squared. 

** Draw centre line at 152.40288736430939554826779524767 degrees for best precision. Precision can be increased beyond this, complementing half the square root of Pi digit-for-digit (arc cosine determines precise angle for the unique right triangle: 62.4028873643.. degree radius, 90 degree left side, 180 degree top side). 

 
Tips:
 
1). Try a circle with a diameter of 2 units (or 20, 200, 2000, etc.) to correlate results directly with half the square root of Pi.
 
2). The 62.4028873643.. degree radius also squares any circle with simple geometry!
 
3). Math reference:
 
  Input half square root of Pi to calculate precise angle:
  acos(0.88622692545275801364908374167057)
  = 27.597112635690604451732204752339 degrees
 
  Subtract from 90 degrees to calculate angle of radius:
  90 - 27.597112635690604451732204752339
  = 62.40288736430939554826779524767 degrees
 
  Add 90 degrees to calculate angle of I-Square center line:
  90 + 62.40288736430939554826779524767
  = 152.40288736430939554826779524767 degrees

R. Holland

BACK

  
Mark Fussell & Stuart Dike