|
Squaring
Berkley Lane
Circle 1 = big outer circle
(black)
Circle 2 = centre circle
standing crop (black)
Circle 3 = outer perimeter of
circle with standing ring (red)
Circle 4 = small circle
standing crop (yellow)
Circle 5 = very small circle
in circle 2
Circle 6 = virtual circle
with midpoint of circle 2 and touching circles 3 and 4 (blue)
Circle 7 = inner perimeter of
the standing ring of circle 3 (green)
Steps to square the circle
(fig. 1, page 3)
1)
Draw the centre axis
through circle 2 and 3 and extend it outside circle 1
2)
Do the same with
circle 2 and 4
3)
Draw a circle around
circle 2 which touches circles 2 and 3 ( circle 6)
4)
Copy outer perimeter
of circle 3 three times to the other axes so, that they are centered and
that their perimeter touches circle 6
5)
Copy circle 4 four
times and put it 'on top' of the circles of step 4 and centre it on the
axes
6)
Draw a square around
the circles of step 5: this is the square that defines the squaring of
the main circle!
And what about the the very
little circle in the centre circle (circle 5)?
Why is it there? What does it
say?
It appears that the distance
of the centre of it to the edge of circle 2 is the radius of circle 3.
Circle 3, copied six times in
circle 2, fits great, forming a flower pattern.
I am also intrigued by the
circle formed by the inner perimeter of circle 3 (the one with the
standing ring) which i will call circle 7.
I wonder if it does have a
function in the total design but now i do not see it.
Update July 13th
(fig. 2, page 3)
After having yesterday's
result I could not stop thinking about this crop circle and every time I
went back to it, stared at it and tried to find more but i did not know
exactly what, until.......
Circle 6, which touches
circles 3 and 4, does not actually exist in the field but on paper it
does and it appears to be an important part of the design.
So would it not be nice to
see if it is possible to square this one as well?
And again i found the
solution!
Draw four lines, each
starting in the corners of the 'big square' and running tangent to
circle 2. The result is squaring the -virtual- circle 6!!
As well as circle 6, the
corner points do not exist in the field but they too form an important
part of the design.
Update July 14th
(fig. 3, page 4)
I think I am going nuts!
I can't keep my thoughts from
this crop circle so this morning i made some prints and again stared at
them for some time.
Suddenly I see something i
have totally overlooked in first instance.
How could I be so
short-sighted?
The tramlines!!
There are four tramlines
cutting the crop circle and i will name them, from left to right in the
picture, A,B,C and D.
Just now I notice that circle
7 (the inner perimeter of the circle with the standing ring) touches
tramline B (the second tramline from the left).
The perimeter of the central
circle (circle 2) touches tramline D (the most right tramline).
Now I see: I found a second
method of squaring circle 6!!
The steps are as follows:
1)
Mark tramline D by
drawing a line touching circle 2
2)
Draw a line tangent to
circle 2 and circle 7: it appears to run parallel to the tramlines and
so parallel to the line of step 1
3) Connect the lines of step
1 and 2 by two lines with 90 degree angles, tangent to circle 2
4) Result: a square and a
second method of squaring the -virtual- circle 6! This square has, of
course, the same size as the square of the first method.
This second method of
squaring the circle (and maybe it should be the FIRST one) is defined by
the tramlines in the field. This reminds me of the Barbury Castle
formation of June 1st 2008 where the public pathway did the
same.
Afterword:
I am quite astonished by what
I found. Squaring the circle: okay, but squaring a virtual circle:
crazy! Finding two methods of squaring the circle: insane!
And then: doubt.......am I
right?
Please don't hesitate to give
your reactions/comments
Rieks
Schreuder
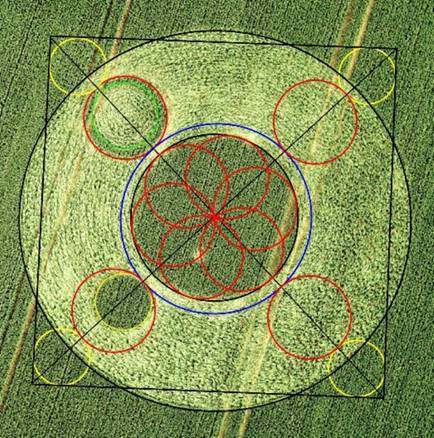
fig. 1
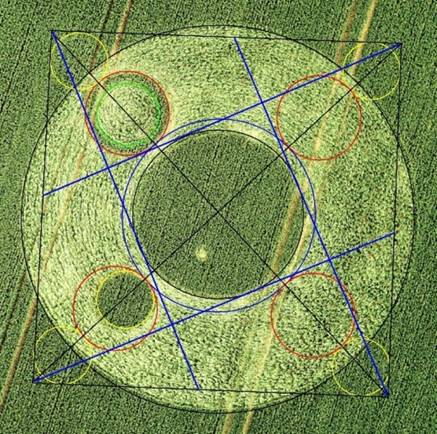
fig. 2
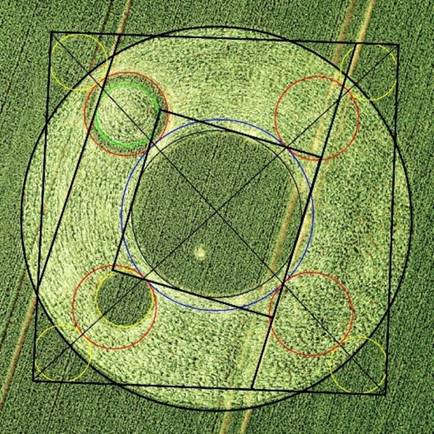
fig.
3 |