Construction and meaning of the crop circle Burrow Hill Fort Rock Lanenr Corley Warwickshire England, 11th July the 2012.  First Step of the construction We see two 12-gon. The inner 12-gon is divided into 12 segments. The segment Z-F-C is the same as C-M-D. So 6 of the 12-gon segments have been set in the outer 12-gon. Let say the outer 12-gon has circum radius 1. Than the area is 3. And 3 is the diameter of a circle true the small spot outside of the circle. 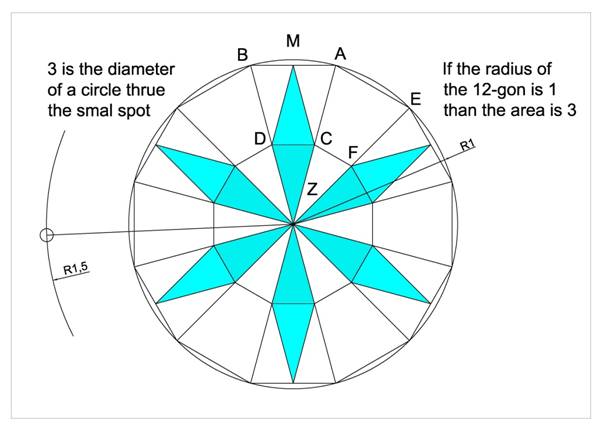Abbildung  SEQ Abbildung \* ARABIC 1 The colored area, the 6 folded star is ¼ of the big 12-gon. One Segment of the 6 folded star is 1/24 of the big 12-gon. (Same areas are Z-C-D, C-A-M, C-M-D, D-M-B and C-A-B-D, F-E-A-C) One can see that the outer point of the 6 folded star is on the inner circle of the 12-gon. Construction of the circles. Phase I (see figure) The inner circle and the outer circle of a equilateral triangle has the proportion 1:2. I have set the inner diameter to 1. Phase II (see figure) Put a square in to the inner circle and set an equilateral triangle on it. The top point of the triangle is on the inner circle of the double outer circles. 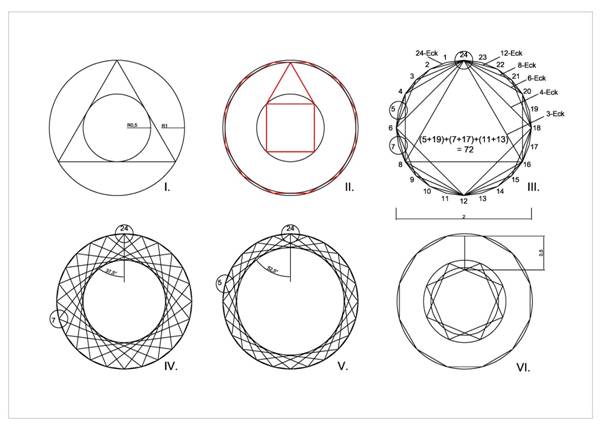Phase III (see figure) Abbildung  SEQ Abbildung \* ARABIC 2 Construct a 24-gon and number the edges as shown. Than you can set the following polygons in it. An equilateral triangle, a square, a hexagon,  an 8-gon, a 12-gon. Now the following edges are free: Edge 1, 5, 7, 11, 13, 17, 19, 23. We discuss it later. The sum of those primes are 48. Phase IV and V (see figure) Set a line from point 24 to the free points 5 and 7. I have set all those lines. The inner circles are those, used for the crop circle. Phase VI (see figure) This is a second kind to construct the circle shown at Phase IV. The calculation of the diameters are very complex. The quotient of the two lines (24-7)/(24-5) is tan(52,5°)=1+(sqrt(3)-1)(sqrt(2)-1). This is not a very useful mathematical expression. But is shows the two numbers sqrt(3) and sqrt(2) and this is interesting in an different sense. Thereto only a short sketch following. 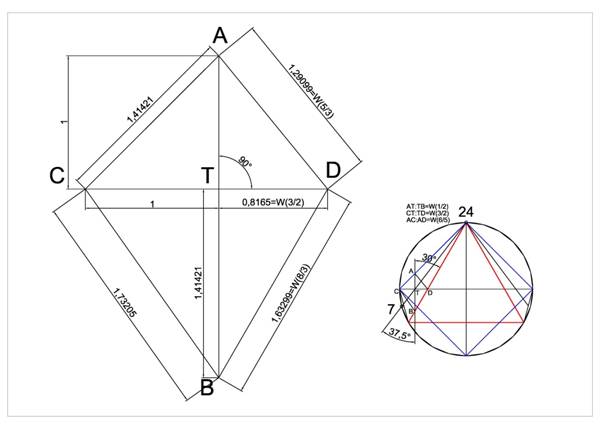Abbildung  SEQ Abbildung \* ARABIC 3 The angle one of the 72 triangle it has the angle 30° and 37,5°, as shown at the sketch. The line 24-7 divides the horizontal and vertical lines between the triangle and the square in an interesting way.  The next picture shows 72 triangles. At the right side you can see the edge numbers which are used for the two middle circles. This edge numbers are tree twin prime. 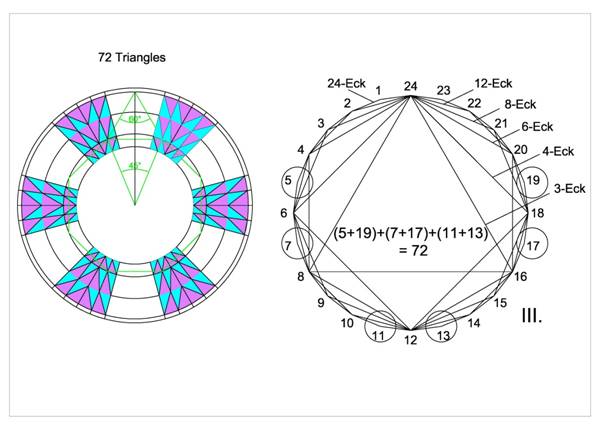Abbildung  SEQ Abbildung \* ARABIC 4 The sum of those three twin primes is 72. This is a hint of Holger Ullmann (http://www.tetraktys.de) Any prime is of the form 6n+1 or 6n-1 (if n is an integer). Therefor all primes are beside the cross points of the 24-gon. It is at the point 6, 12, 18 and 24. Each squared prime number minus 1 is divisible by 24, if the prime is larger 3 5 ·   5 – 1 =   24 =   1 · 24  7 ·   7 – 1 =   48 =   2 · 24 11 · 11 – 1 = 120 =   5 · 24 13 · 13 – 1 = 168 =   7 · 24 17 · 17 – 1 = 288 = 12 · 24 19 · 19 – 1 = 360 = 15 · 24 ...( Holger Ullmann) The mathematical proof by Werner Brefeld  (http://www.brefeld.homepage.t-online.de/teilbar-24.html): p-1, p, p+1 are tree successive numbers and one of it must be divisible by 3. P can not be divisible by 3 because p is a prime greater than 3. Therefor p-1 or p+1 must be divisible by 3 p is a prime and an odd number therefor P-1 and p+1 must be divisible by 2. Every second number which is divisible by 2 must be divisible by 4. Therefor (p-1)(p+1) must be divisible by 8. A number which is divisible by 3 and 8 is also divisible by 24, because 3 x 8 = 24 QED. The cross totals of the Fibonacci numbers repeated every 24 times. 21.12.2012 Willibald Limbrunner