Wayland’s Smithy Long
Barrow (2) – reported 12 August 2009
FURTHER THOUGHTS (5
September 2009)
The image initially
seemed to me not a Rose Window, but the interior of a large Dome. I felt
as if I was being invited to look upwards and outwards, and to gain a
deeper awareness of what lies “out there” in the dome of the cosmos, and
to think about our earthly relationship with this. With this feeling, I
was sure that this formation would inevitably conceal yet another clever
Squaring of the Circle. Indeed, it turns out that the method described
by Bert Janssen (at
200803) applies also to this formation. But the key to
revealing it lies geometrically beneath the surface, and some
deconstruction is required in order to show it. The pattern in the outer
segment is comprised of circles and four-leaf foliage symbols. In fact
the latter are (geometrically) quadruple viscera Pisces in which the
revealed circles turn out cleverly to fill the overall space between the
two darker rings. This can be seen in Figure 1.

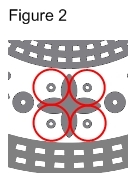
It will be seen,
however, that the four smaller circles surrounding each viscera Pisces
do not occupy the exact centres of these new circles –each is slightly
offset outwards from the overall centre of the complex.
In fact, it turns out
that these smaller circles each mark the centre of yet a further set of
four “invisible” circles that also cleverly fill the space between the
two darker rings. These fit snugly together, and present a new size of
circle that does not visibly appear elsewhere in the formation. This can
be seen in Figure 2.
While (as will be
seen) this new circle is of great structural importance to the geometry,
those former circles that form the viscera Pisces are not – they remain
merely “artistic”. So the whole presentation is a mix of subtle
mathematics and pure artistry (though these remain cleverly
interlinked!).
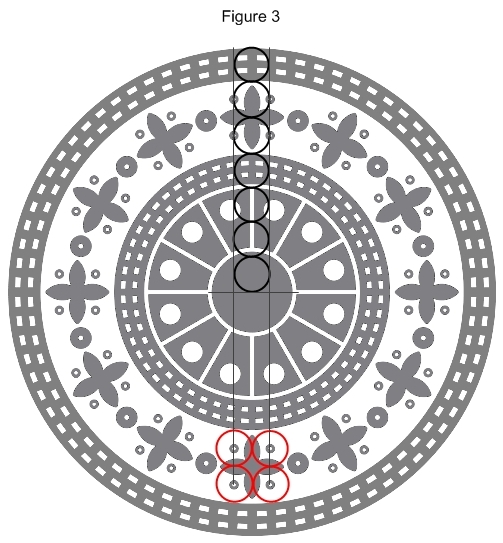
This new size of
circle is such that it exactly fits the overall radius of the formation
7 times. This can be seen in Figure 3.
Following the method
outlined by Bert Janssen (see above link), if the overall radius of the
formation is deemed to be “1”, then its overall circumference will equal
2 x Pi. For a square to have the same perimeter as the circle, each of
its sides must have a value of 11/7, the four sides together thus
equalling 2*(22/7). This will mean that half the length of one side will
equal 5.5/7.
So, of the seven
stacked circles in Figure 3, the point midway between the end of circle
5 and the end of circle 6 will mark the position (5.5/7) of the edge of
the square being sought. This “5.5/7” position coincides with remarkable
clarity (and pleasing inevitability) with the positions of the two outer
small circles that surround the four-leaf patterns.
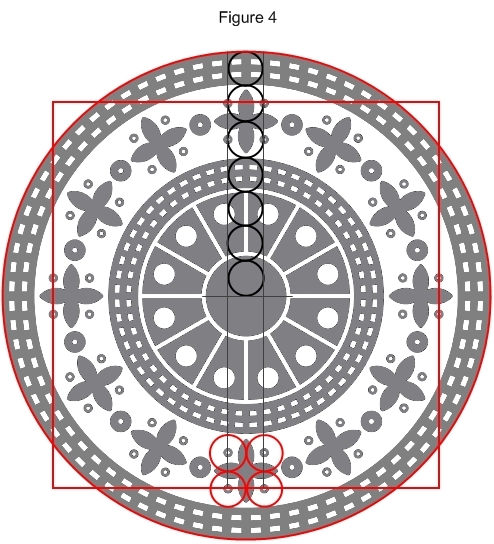
Figure 4 shows how,
from this geometric construction, the squaring of the circle is
achieved.
Such a formation is
too complex to have been laid overnight by hoaxers:
a) it would require
marking out 48 “invisible” circles to construct the 12 viscera Pisces;
b) it would require the similar marking out of a further 48 “invisible”
circles to determine the centre points marked by the small circles
surrounding the viscera Pisces in the formation; c) these latter
“invisible” circles would have needed to be the starting point for the
entire formation, since overall the diameter would have had to
accommodate exactly 14 of them (even though they will never appear
anywhere in the finished product).
The simplest way of
creating the formation would be exactly as I have done here: create the
diagram in full, and then simply remove from it all the components that
are to be kept “secret”. Then from the Print Menu, select from the list
of Options “Print to Selected Crop Field”. Unfortunately since there is
not, and never has been, such an advanced option (even in the latest
version of Vista) one can only assume that it was “printed” to the field
by a technology completely unknown to us!
Roger Wibberley |