Schijn bedriegt!

Door Richard van Rijswijk

HET IS VERDOBEN DOOR DE BOER HET VELD TE BETREDEN!!

In de nacht van 5/6 juli is er in Nederland een mooie graancirkel verschenen. Zo op het eerste gezicht leek het een simpele cirkel met wat onbeduidende getallen en zelfs een asymmetrisch eivormig midden. Maar als we wat dieper op de gegevens ingaan die daar ter plekke zijn gemeten, betreden we de bijzondere wereld van de Heilige Geometrie waarbij niets, niets voor niets is!

Peter Vanlaerhoven berichte mij vorige week dat hij voor de 2^e keer het graanveld in Standdaardbuiten in was gegaan voor onderzoek omdat daar volgens Robbert van den Broeke nog een formatie was ontstaan na de al eerdere formatie van die week daarvoor in het zelfde veld. Er bleek inderdaad weer een nieuwe graancirkel te liggen en Peter vertelde mij dat het deze keer om een meer geometrisch patroon leek te gaan, een aantal grote cirkels en wat losse kleinere cirkels. Ik wachte in spanning de afmetingen en de details van deze nieuwe cirkel af. Toen ik deze eenmaal onder ogen had sprongen er voor mij direct twee getallen uit. Eén daarvan was 72 (diameter grote cirkel) en een andere was 1,6 (diameter van de kleinste cirkel onder) die ik al snel met het getal 1,618 geassocieerde. Dit getal is beter bekend als het getal Phi en wordt ook wel de Gulden Snede genoemd. Het getal 72 is het aantal graden van meerdere hoeken in een pentagram, een geometrisch figuur waar de Gulden Snede ook veelvuldig in terug is te vinden. Het getal 72 is dan ook onafscheidelijk van het getal Phi.  

Mijn aandacht was dus door deze getallen getrokken en ik begon dan ook direct te tekenen en op onderzoek uit of mijn vermoedens werden bevestigd door deze getallen terug te vinden waren binnen de formatie. Natuurlijk begon ik met een pentagram binnen in de grote cirkel van 72 meter te tekenen. Hieronder heb ik mijn verdere ontdekkingstocht door de cirkel heen weergeven in beeld zodat u het stap voor stap mijn ontdekkingstocht door deze formatie kan mee beleven. 

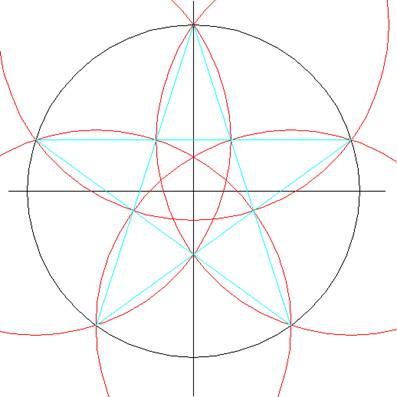
De grote zwarte cirkel is de cirkel van 72 meter. Hierin de hulpcirkels (rode) getekend om uiteindelijk het pentagram (blauw) te kunnen tekenen 

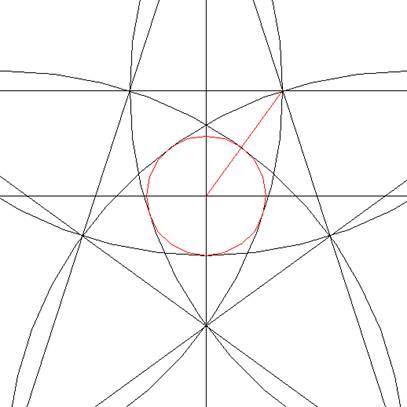
Vanuit het middelpunt naar één van de binnenhoeken van het pentagram en lijn trekken en daar waar de lijn de eerste cirkel tegenkomt een cirkel trekken vanuit het middelpunt tot dat snijpunt. Je hebt nu, op een paar centimeter nauwkeurig, de cirkel met een diameter van 12,5 meter gevonden.

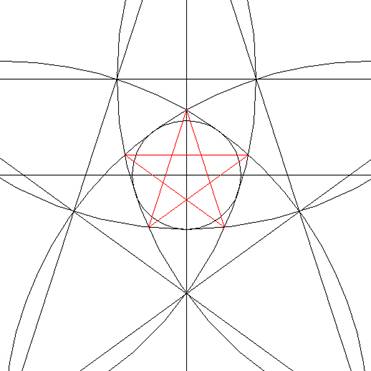
We verbinden nu de snijpunten van de hulpcirkels met elkaar die het dichtste bij het middelpunt liggen. Hierdoor krijgen we wederom een Pentagram. Deze pentagram hebben we later in de tekening weer nodig als hulplijnen en laten we dus nu even met rust.  

Nu trekken we wederom een nieuw pentagram, maar nu verbinden wij alle binnenhoeken van het grote pentagram die we als eerste hebben gemaakt bij de grote cirkel van 72 meter in doorsnede.

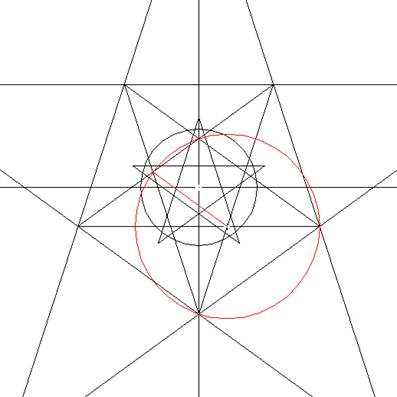
Vanuit één van de binnenhoeken van deze nieuwe pentagram trekken we een cirkel naar het bijna tegenoverliggende binnenhoek (zie de rode lijn als maat van de denkbeeldige passer). 

Nu trekken we vanuit het middelpunt een lijn (rood) naar de punt van dat pentagram en waar de lijn de zojuist gemaakte cirkel elkaar kruisen maak je vanuit het middelt nog een cirkel (rood). U hebt zojuist de buitenlijn gevonden van de 9 (+ 20-25 cm)meter cirkel!

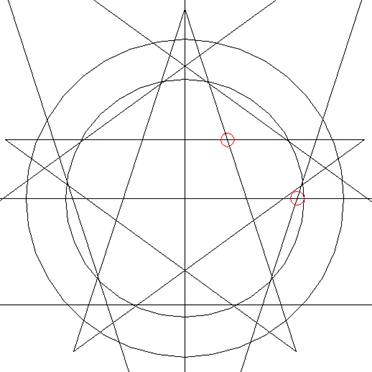
Nu plaatsen we, aan de kant waar het middelgrote pentagram de middellijn kruist, een cirkel (rood rechts) die loopt vanaf dat kruispunt tot het punt waar de middellijn de zojuist getrokken 9 meter cirkel kruist. Dan pakken we deze zelfde cirkel op en trekken dezelfde cirkel in de binnenhoek van het kleine pentagram. 

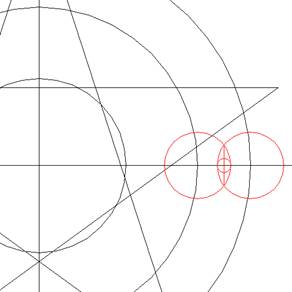
Vanuit dit punt trekken we een lijn (rood) naar het middelpunt en dan trekken we vanuit dit zelfde middelpunt een cirkel die een grootte heeft van waar de zojuist getrokken lijn en de kleine cirkel elkaar kruisen. U hebt zojuist de cirkel getrokken met een diameter van 5,2 cm welke de totale breedte was van het ei in het midden!!

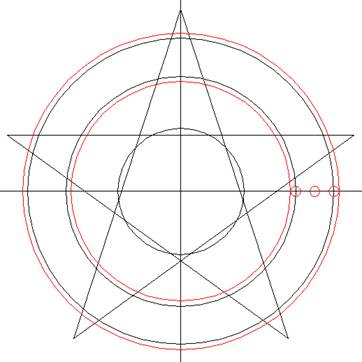
Toen ik een flinke avond had gestoeid met lijnen en cirkels liep ik geheel vast met een beeldscherm die eruit zag als een bord spaghetti. Ik besloot het allemaal te laten rusten en lekker te gaan slapen. De volgende ochtend tussen waken en slapen in kreeg ik een duidelijk beeld voorogen dat de onderste 3 kleinere cirkel de sleutels waren van de gehele formatie. Hiermee ging ik dus direct mee aan de slag en veegde alle lijnen weer van het beeldscherm totdat het bovenstaande beeld overbleef. Wanneer we de twee 2 meter cirkels (van de 3 kleinere cirkels) op bovenstaande manier plaatsen en het overlappende gedeelte opvullen met een cirkel zien we tot onze verbazing dat de helft van de bal zo’n dikke 20 cm is…wat de gemiddelde breedte is van de getrokken cirkels!  

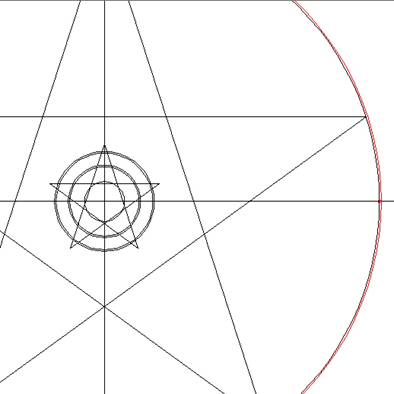
Wanneer we deze afmetingen verschuiven over de lijn en de binnen en buitenlijnen afmaken van de reeds gevonden cirkels, zijn deze nu compleet.

Dit doen we uiteraard ook bij de grootste cirkel hé! 

Nu trekken we een lijn (rood) van de twee snijpunten van het pentagram en de kleinste cirkel van 5,2 meter. Vanuit het middelpunt trekken we een cirkel (rood) tot aan deze lijn.

(even iets extra maar niet geheel onbelangrijk) Tot mijn grote verbazing trok ik deze lijnen even door en bleek dat we hieruit een 99.99999% zuiver vierkant kregen??? En wat ik helemaal vergeet te vertellen is dat deze cirkel nagenoeg een diameter heeft van 3,7 meter?? Een van de diameters gemeten in het ei!!

Deze schuiven we dus langs de as keurig netjes op de plek waar deze is gemeten.

Als we nu vanuit het middelpunt een cirkel trekken tot het punt waar de vorige cirkel (groen) de hartlijn raakt dan krijgen we een cirkel (rood) van 3,4 meter?? Dat is de andere diameter die Peter had gemeten in het ei!! Is het niet fantastisch, de antwoorden liggen gewoon klaar…

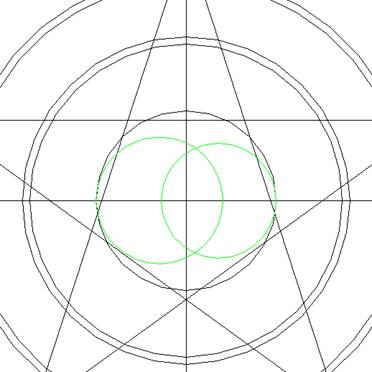
Dan schuiven we die ook maar op zijn plek waar deze was gemeten.

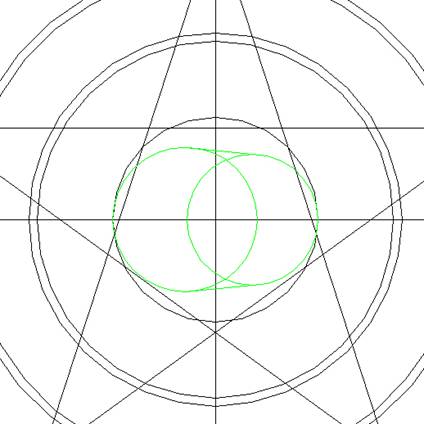
Nu nog de cirkels onder en boven met elkaar verbinden en we hebben onze eivorm herleid!!! 

Even in zwart/wit voor het plaatje helder te krijgen.

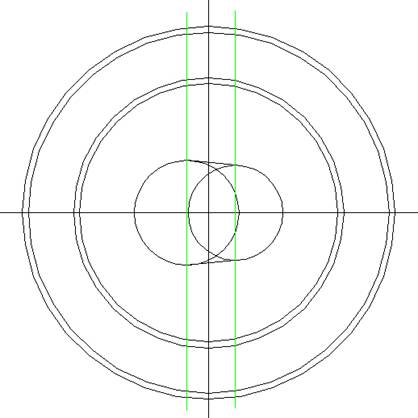
Over de middelpunten van de zojuist gemaakte cirkels trekken we een verticale lijn, die (zijn niet gemeten) niet veel kunnen schelen qua ligging met de tractorsporen in het veld. Het zal mij in ieder geval niet verbazen!

Zo ziet het geheel er dan uit, maar dan missen we toch nog de sleutels tot het geheel. 

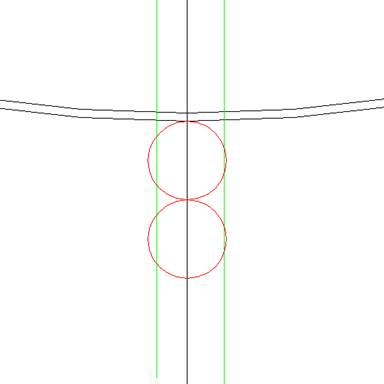
Daarvoor gaan we helemaal naar beneden en trekken daar twee cirkels van 2 meter naar beneden, zoals de sleutels zelf aangeven. (Dit is dus de tweede keer dat we de twee 2 meter cirkels letterlijk gebruiken)

Breedte van de 72 meter cirkel

Vervolgens trekken we vanuit het middelpunt weer een cirkel (rood), alleen deze keer tot het snijpunt van de onderste 2 meter cirkeltje en de verticale as van de formatie.

Vervolgens zetten we op deze nieuwe grote cirkel 3 x de 2 meter cirkeltjes uit waarvan de meest rechtse (de zwarte) er ook daadwerkelijk ligt in het veld!

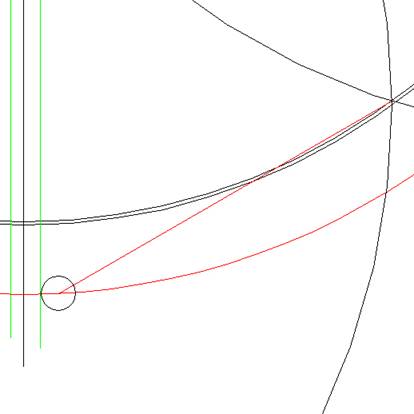
Nu trekken we vanuit dat middelpunt van deze cirkel tot aan een poot van de in stap 1 getekende pentagram en zijn hulpcirkels een lijn.

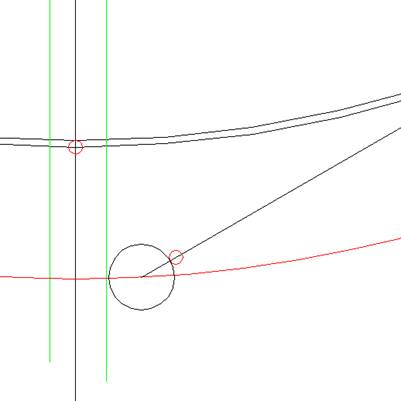
Op de lijn zetten we weer de oorspronkelijke cirkel neer die we eerder ook al hadden gevonden en de breedte van de lijnen van de cirkels had bepaald. 

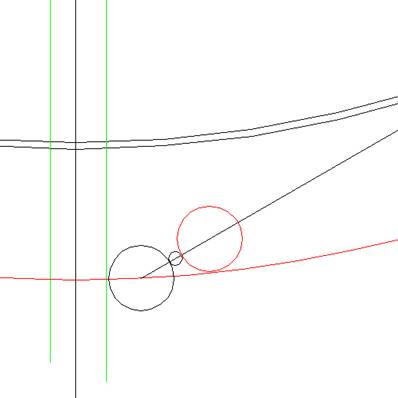
Vervolgens weer een 2 meter cirkel en daar is de tweede 2 meter cirkel op zijn juiste plek.

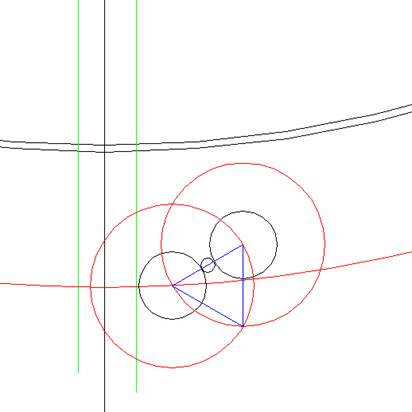
Nu trekken we de twee rode cirkels, waardoor we een gelijkzijdige driehoek (blauw) kunnen maken.

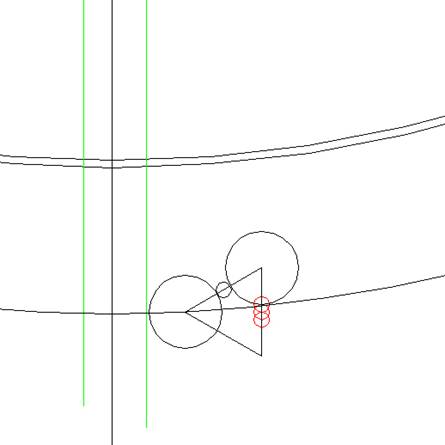
Nu trekken wij drie maal op deze driehoek het oorspronkelijke cirkeltje (rood) weer.

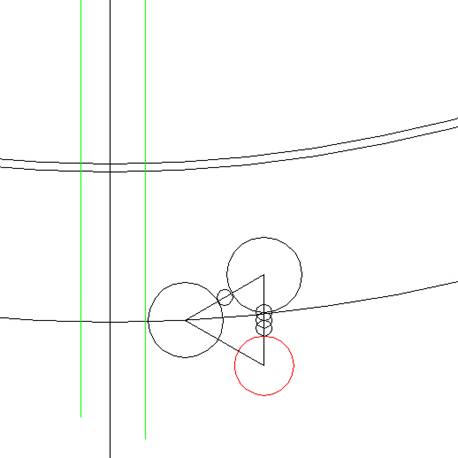
En dan vanuit de nog lege hoek van de gelijkzijdige driehoek trek je een nieuwe cirkel (rood) tot aan het snijpunt van de driehoek en het laatst getrokken oorspronkelijke cirkeltje. 

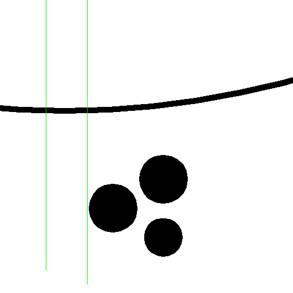
Resultaat voor het plaatje…altijd leuk en duidelijk. 

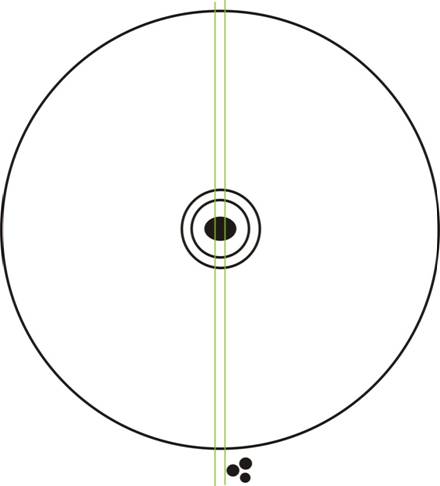
En dan uiteindelijk de gehele formatie inclusief tractor sporen in het midden.

en nog een toetje van de makers….

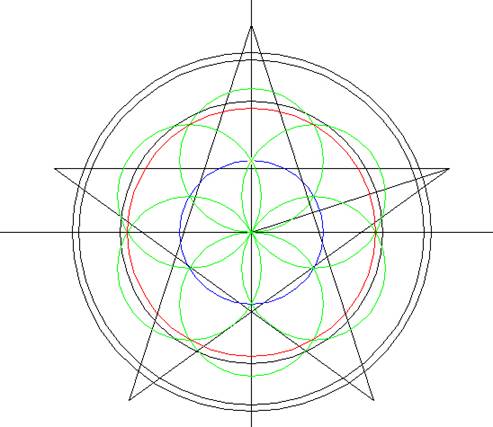
We hebben tot nu toe gezien dat alles elkaar redelijk goed opvolgt, maar wat mij nog nooit is overkomen is dat een geometrisch patroon dat voornamelijk wordt opgebouwd met pentagrammen terug kan worden herleid met andere geometrische basispatronen. Maar ik hou jullie niet langer in spanning. Wanneer je de cirkel van 5,2 meter (blauw) als basis neemt en hiermee een Seed of Life (groen en blauw) construeer en een cirkel (rood) vanuit het middelpunt trekt tot aan waar de buitencirkels van de Seed of Life elkaar kruisen… dan krijg je exact de 9 meter cirkel!!!   

Een woord  tot de makers van deze cirkel.

Als iemand dit zelf verzonnen heeft en in het graan heeft gemaakt en ook nog bij zijn volle verstand, dan heeft hij of zij dit heel erg knap gedaan en er een leuk reken-worstelpartijtje van gemaakt om te ontcijferen (zonde trouwens van de schade voor de boer!!!). Mocht je dit toevallig hebben gemaakt en lukraak wat afstanden in de plank hebben genomen, dan moeten we toch eens praten want dan heb je bijzondere natuurlijke aanleg voor Heilige Geometrie (Maar nog steeds zonde van de schade voor de boer!!!).

Maar zelf denk ik vanuit mijn bevindingen van de opbouw van deze graancirkel, dat het constructief onmogelijk is geweest dit ook daadwerkelijk zo uit te meten in het veld, zoals hierboven beschreven. Dan vervolgens ook nog eens de cirkel te maken zonder daardoor sporen achter te laten in of om het gewas is wel heel bijzonder. Natuurlijk was het in dit geval ook wel allemaal uit te rekenen cirkel voor cirkel, maar wat een ongelofelijk rekenwerk zeg voor 6 cirkeltjes en ei….

Petje af voor de makers en scheppers van deze graancirkel!

O ja, ik wilde ook nog een opmerking plaatsen over de wisselende temperatuur en energie schommelingen die Peter en Sjaak daar voelde in de cirkel. Mijn ervaring in een geometrisch symbool te lopen die voornamelijk is opgebouwd uit pentagrammen sluit zich hierbij volledig aan. Mijn ervaring hierin heeft geleerd dat de Gulden Snede, het pulserende Hart van ons universum, deze pulsering gewaar kan maken wanneer je jezelf daarvoor open stelt.

Verder moet ik zeggen wanneer je deze cirkel natekent zoals ik hier boven heb gedaan ongetwijfeld net wat afwijkende afmetingen krijg die niet verder op zullen lopen dan zo een 5 cm. Op een grote van de gehele formatie is dit een afwijking van 0.0069% en mag worden verwaarloosd. 

Laatste update tweede bezoek: 

Bij het tweede bezoek aan de graancirkels hebben we na aanleiding van de bovenstaande reconstructie nog een afmeting onderzocht. De vraag was namelijk of dat het onderste snijpunt van de hulpcirkels van het eerste pentagram iets te maken had met de eerste formatie in het zelfde veld.

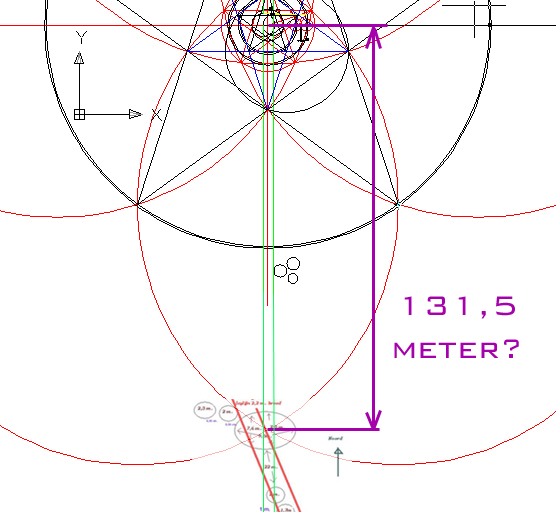
Toen we gingen meten bleek dit inderdaad zo te zijn. Dit snijpunt liep exact door een cirkel van de eerste formatie…..toeval? ik laat het aan u over! Zie de afbeeldingen hieronder voor meer details hierover. Ik heb hiervoor de overzichttekening van Peter van cirkel 1 over de tekening van cirkel 2 gelegd. Kijk eens naar de toevalligheden die gaan ontstaan. Ook de afmetingen van de eerste formatie hebben overeenkomsten met de tweede.

 In Lak’ech

Richard van Rijswijk

Meer informatie over Heilige Geometrie www.detaalvanhetlicht.nl