Reconstruction of the
2011 Temple Farm formation |
|
| 1. |
| Draw a circle. Draw the horizontal and vertical centerlines.
|
|
| 2. |
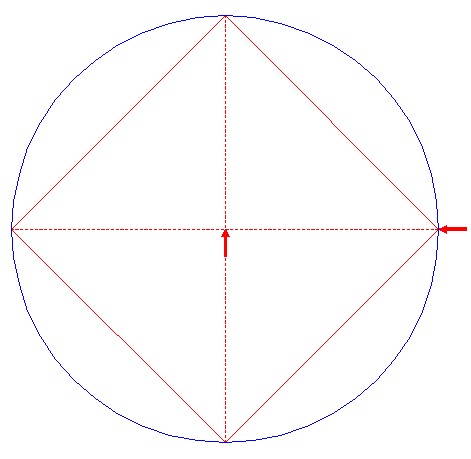
| Construct the inscribed square of circle 1, pointing to the right.
|
|
| 3. |
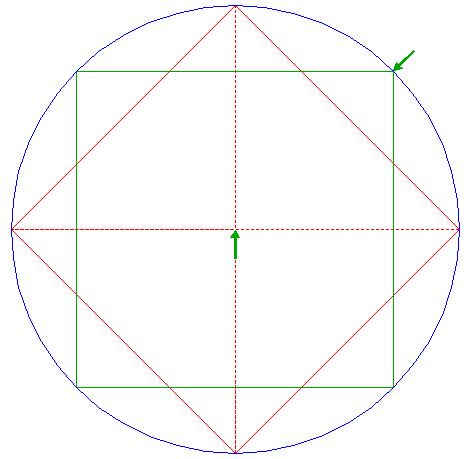
| Construct the inscribed square of circle 1, sides horizontal and vertical.
|
|
| 4. |

| Construct the inscribed octagon (regular 8-sided polygon) of circle 1, pointing to the right.
|
|
| 5. |
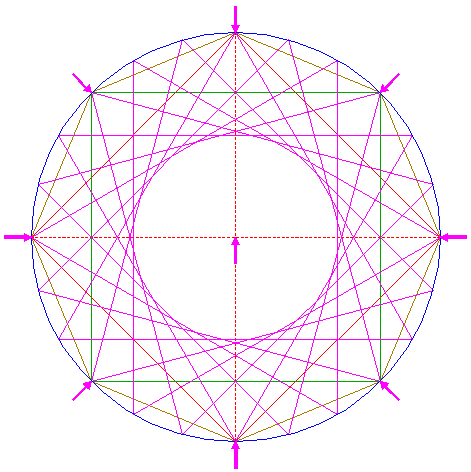
| Construct eight inscribed equilateral triangles of circle 1, each with one angular point coincident with successive angular points of octagon 4, as shown.
|
|
| 6. |
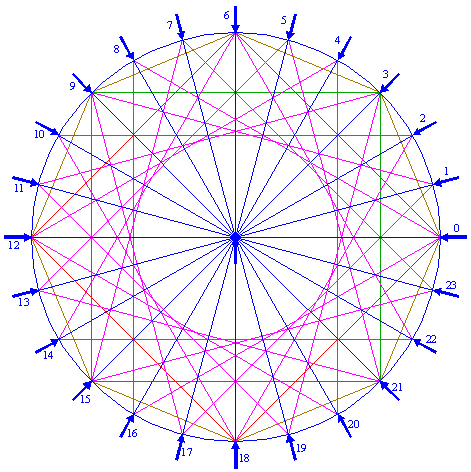
| Draw 24 rays from the center of circle 1 to all angular points of triangles 5. Number these rays counterclockwise from 0 to 23, starting at the rightmost one, as shown.
|
|
| 7. |
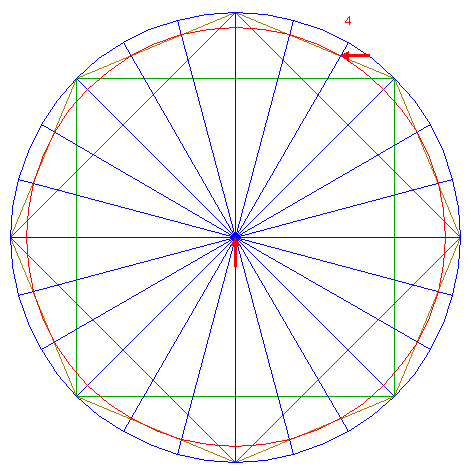
| Construct a circle concentric to circle 1, passing through the intersection of ray 6 nr. 4 and the upper righthand side of octagon 4.
|
|
| 8. |
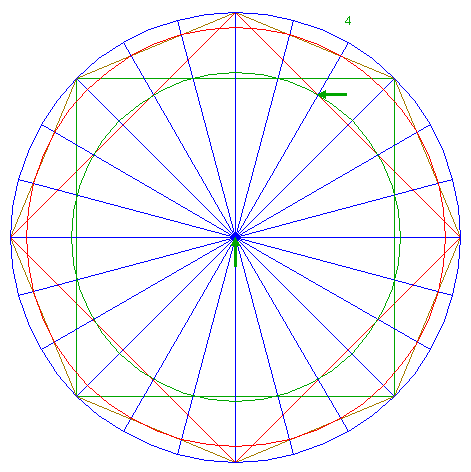
| Construct a circle concentric to circle 1, passing through the intersection of ray 6 nr. 4 and the upper righthand side of square 2.
|
|
| 9. |
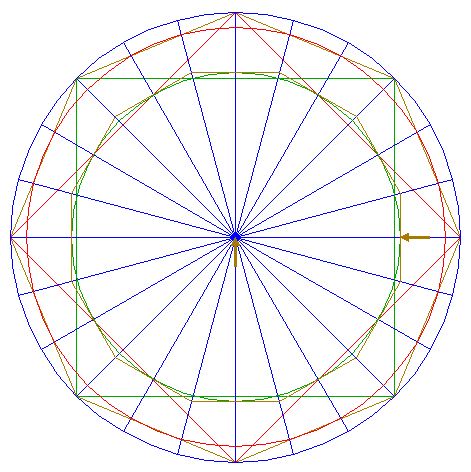
| Construct the circumscribed dodecagon (regular 12-sided polygon) of circle 8, with the midpoint of one side coincident with the righthand intersection of circle 8 and the horizontal centerline.
|
|
| 10. |
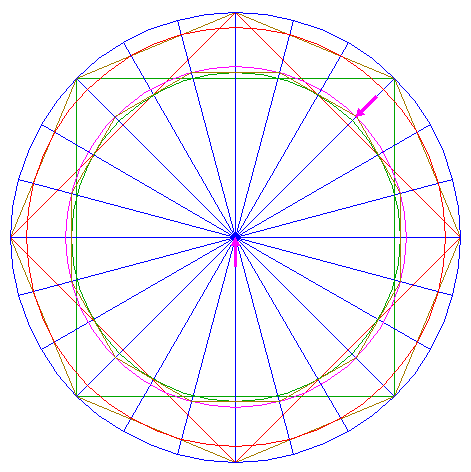
| Construct the circumscribed circle of dodecagon 9.
|
|
| 11. |
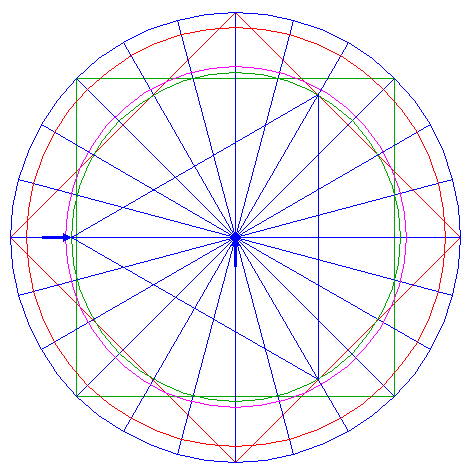
| Construct the inscribed equilateral triangle of circle 8, pointing to the left.
|
|
| 12. |
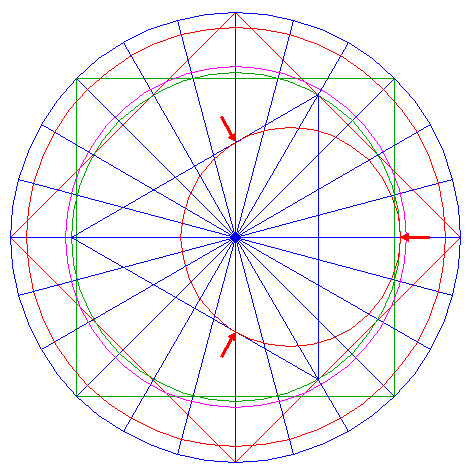
| Construct a "three-points" circle, passing through the righthand intersection of circle 8 and the horizontal centerline, and passing through the intersections of the lefthand sides of triangle 11 and the vertical centerline.
|
|
| 13. |
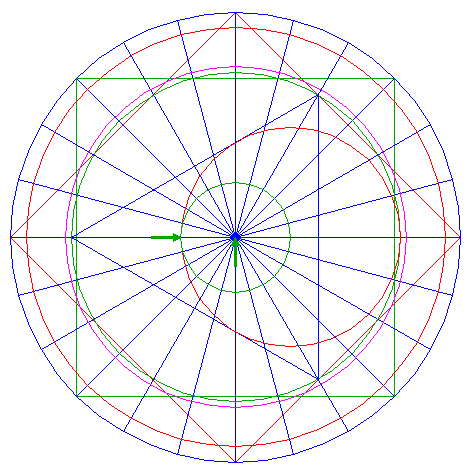
| Construct a circle concentric to circle 1, tangent to circle 12 at the lefthand side.
|
|
| 14. |
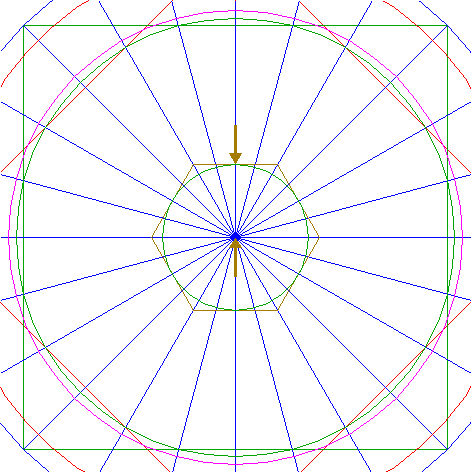
| Construct the circumscribed hexagon (regular six-sided polygon) of circle 13, pointing to the right.
|
|
| 15. |

| Construct the circumscribed circle of hexagon 14.
|
|
| 16. |
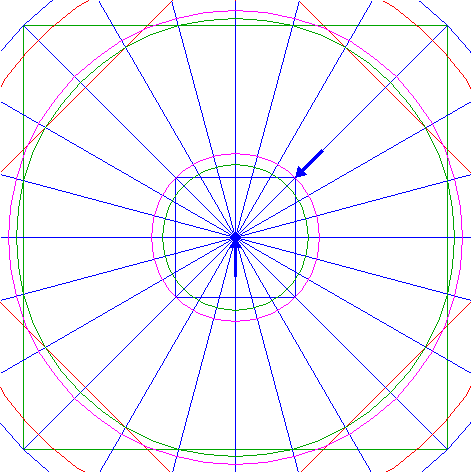
| Construct the inscribed square of circle 15, sides horizontal and vertical.
|
|
| 17. |
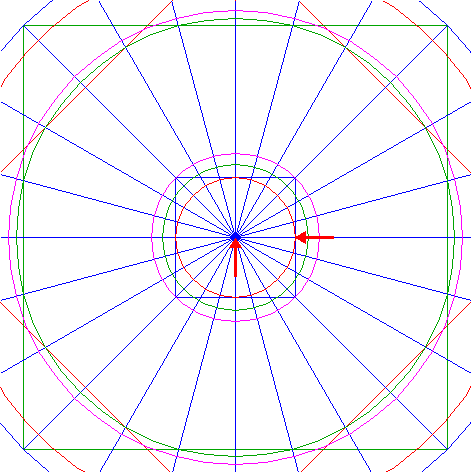
| Construct the inscribed circle of square 16.
|
|
| 18. |
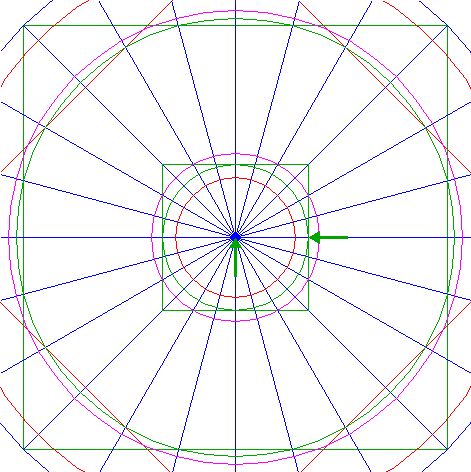
| Construct the circumscribed square of circle 13, sides horizontal and vertical.
|
|
| 19. |

| Construct the circumscribed circle of square 18.
|
|
| 20. |
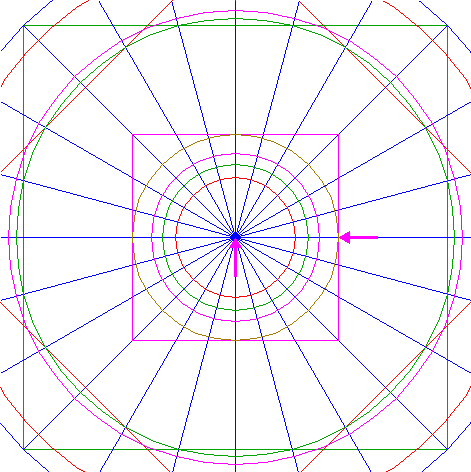
| Construct the circumscribed square of circle 19, sides horizontal and vertical.
|
|
| 21. |
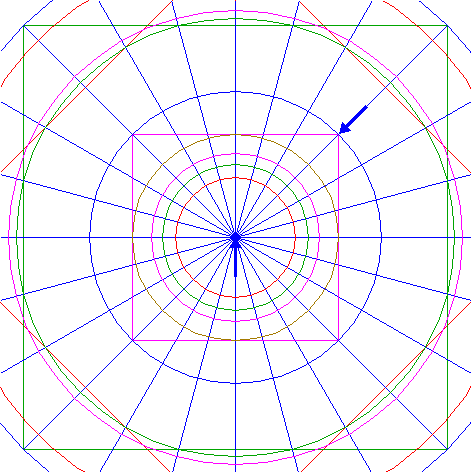
| Construct the circumscribed circle of square 20.
|
|
| 22. |
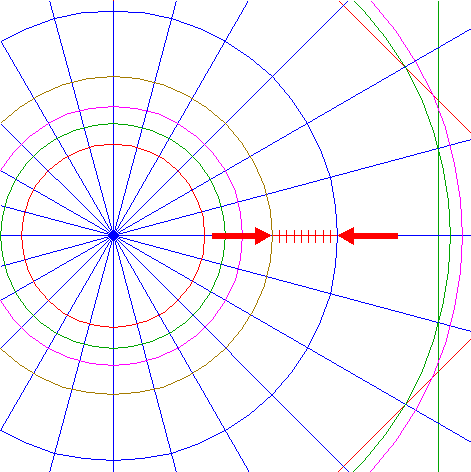
| Divide the linesegment in between the righthand intersections of circles 19 and 21 with the horizontal centerline into nine equal parts.
|
|
| 23. |
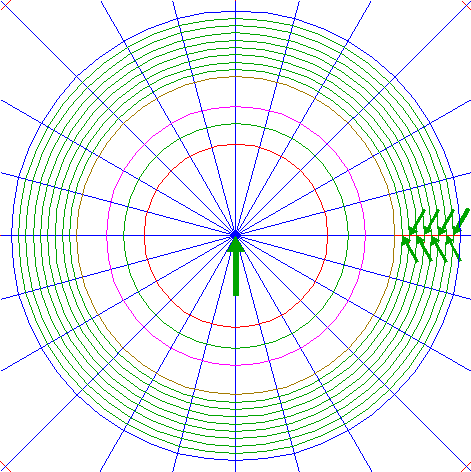
| Construct eight circles concentric to circle 1, passing through the dividing nodes 22, as shown.
|
|
| 24. |
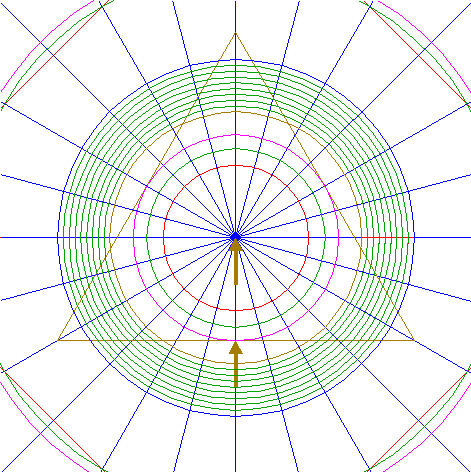
| Construct the circumscribed equilateral triangle of circle 15, pointing up.
|
|
| 25. |
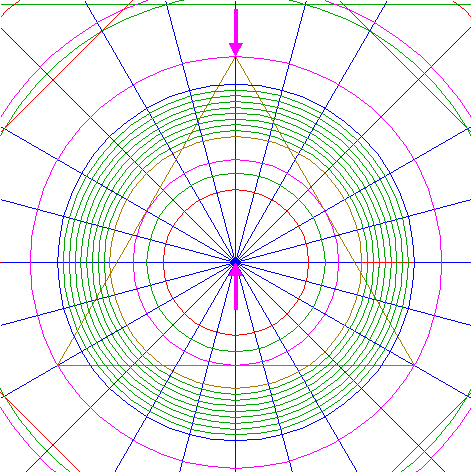
| Construct the circumscribed circle of triangle 24.
|
|
| 26. |
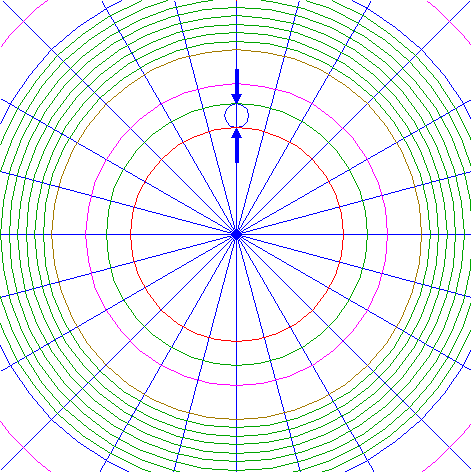
| Construct a "two-points" circle (defined by the two end-points of a centerline) between the upper intersections of circles 13 and 17 with the vertical centerline.
|
|
| 27. |
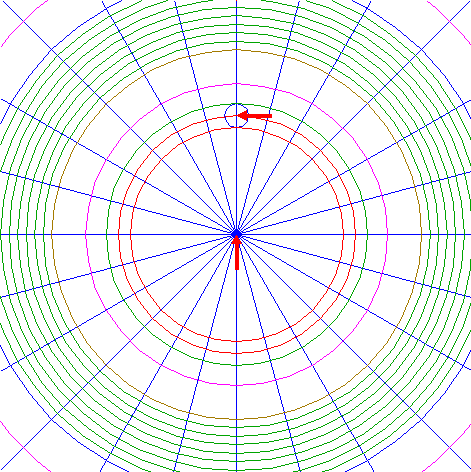
| Construct a circle concentric to circle 1, passing through the center of circle 26.
|
|
| 28. |

| Draw the connecting line between the center of circle 1 and the intersection of the upper righthand side of square 2 and the righthand side of square 3.
|
|
| 29. |
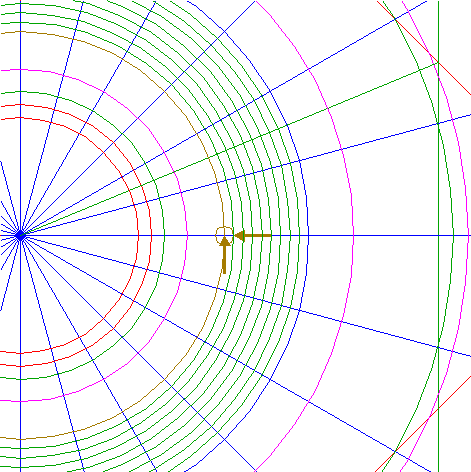
| Construct a circle centered at the righthand intersection of circle 19 and the horizontal centerline, tangent to the innermost circle 23 at the near side.
|
|
| 30. |

| Copy circle 29 to the intersection of circle 27 and line 28.
|
|
| 31. |

| Construct a "two-points" circle between the center of circle 30 and its righthand intersection with line 28.
|
|
| 32. |
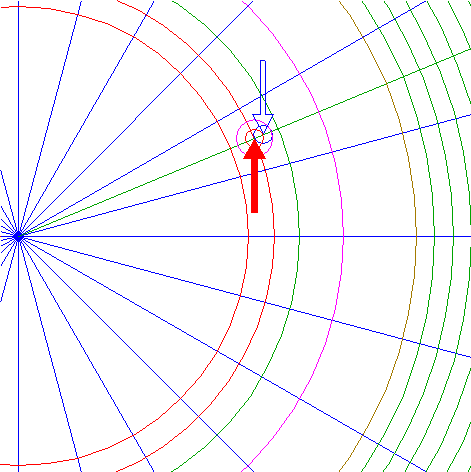
| Copy circle 31 to the center of circle 30.
|
|
| 33. |
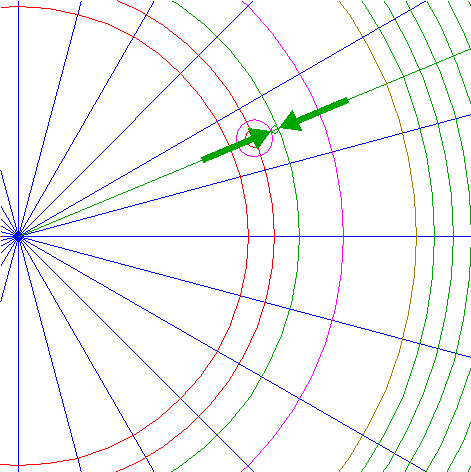
| Construct a "two-points" circle between the righthand intersections of circles 30 and 13 with line 28.
|
|
| 34. |

| Copy circle 33 four times, to the center of circle 1, and to the intersections of circle 1 with rays 6 nrs. 0, 1 and 2.
|
|
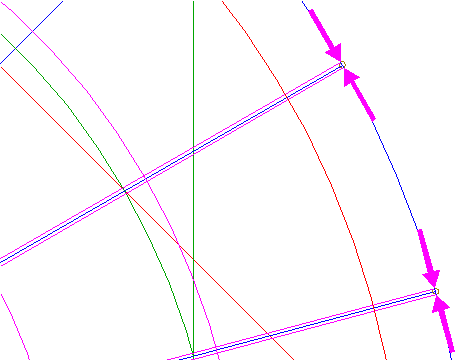
| 35. |

| Draw three pairs of parallel lines, each tangent to the central circle 34, and tangent to the peripheral circles 34 successively, each time at both sides. See details.
|
|
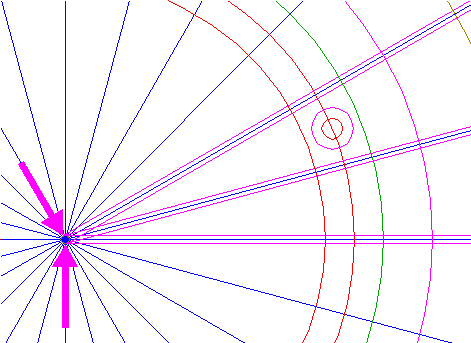
|
|
|
|
| 36. |
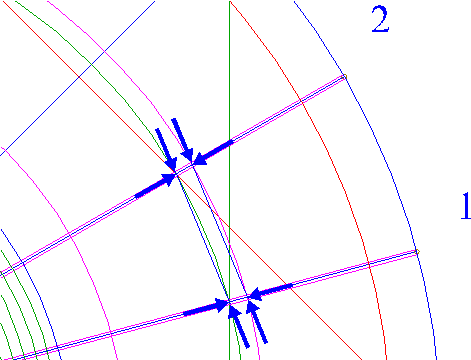
| Draw two connecting lines, between the intersections of rays 6 nrs. 1 and 2 with circle 8, and with circle 10. Extend these lines in both directions upto the nearest line 35.
|
|
| 37. |
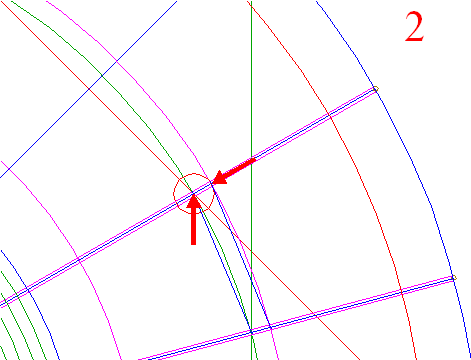
| Construct a circle centered at the intersection of circle 8 and ray 6 nr. 2, tangent to circle 10 at the near side.
|
|
| 38. |

| Copy circle 37 to the center of circle 1.
|
|
| 39. |

| Draw a line, tangent to circles 37 and 38 at the lower sides.
|
|
| 40. |
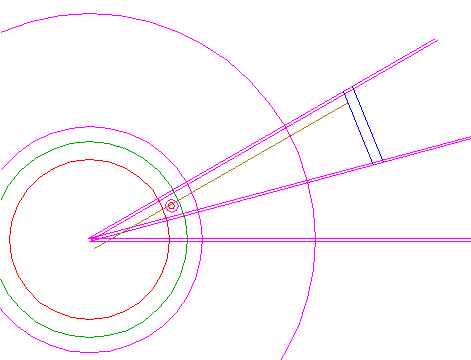
| Remove all parts from circles 13, 15, 17, 25, 30 and 32, and lines 35, 36 and 39, until the shown pattern remains.
|
|
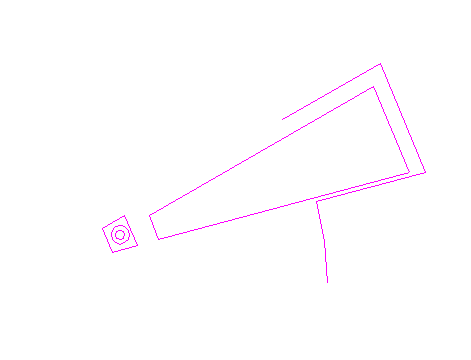
|
|
| 41. |
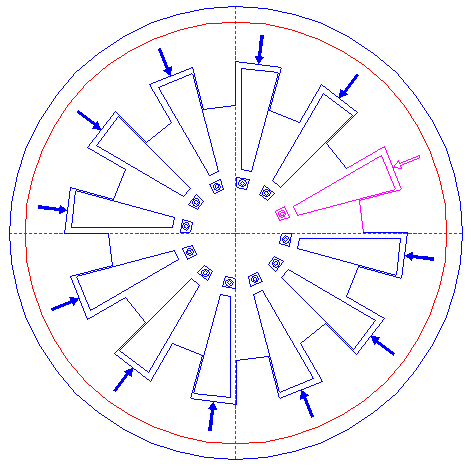
| Copy pattern 40 eleven times, while rotating them around the center of circle 1, and, together with pattern 40 itself, distributing them evenly around the circle (each time 30° in between).
|
|
| 42. |

| Remove all parts from circle 21, and lines 35, until the shown pattern remains.
|
|
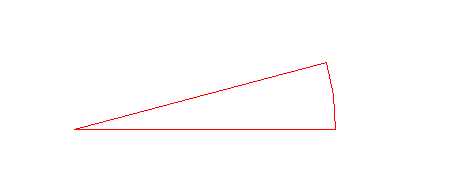
|
|
| 43. |
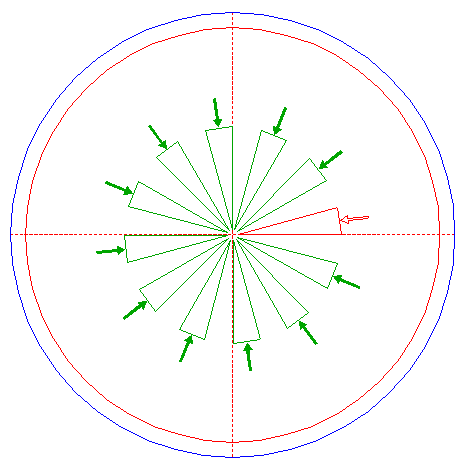
| Copy pattern 42 eleven times, in the same way as pattern 40 in step 41.
|
|
| 44. |
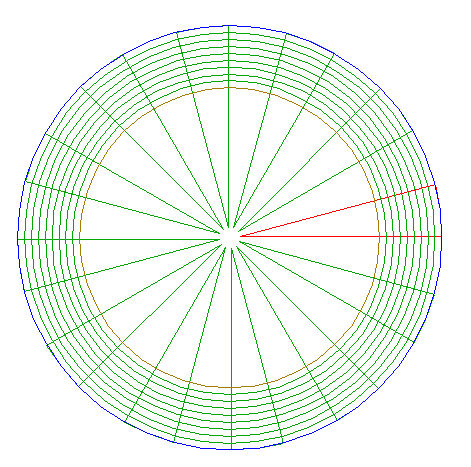
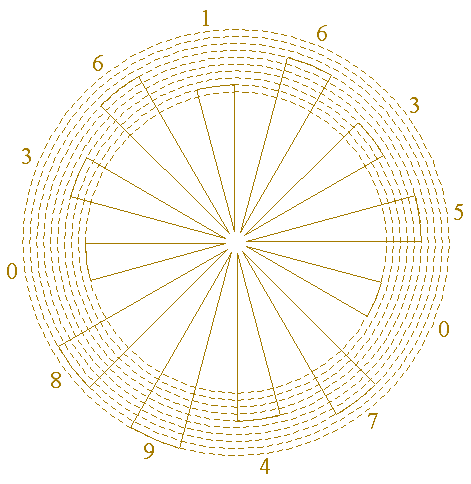
| Remove all parts from circles 19, 21 and 23, and patterns 42 and 43, until the shown pattern remains.
When circles 19, 21 and 23, are given the values 0 through 9 from inside outwards, the remaining pattern represents the following values, starting from the "largest", clockwise: 9, 8, 0, 3, 6, 1, 6, 3, 5, 0, 7, 4.
|
|
|
|
| 45. |
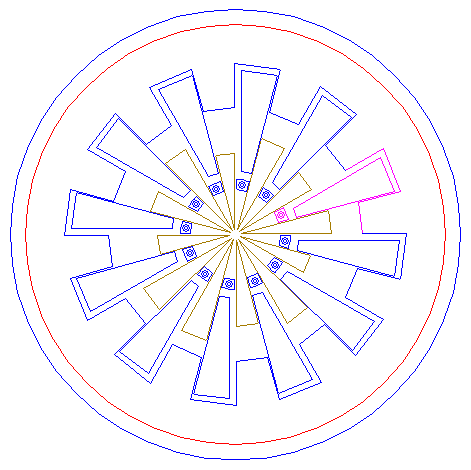
| Circles 1 and 7, and patterns 40, 41 and 44, together, make up the final reconstruction.
|
|
| 46. |

| Colour all areas corresponding to standing...
|
|
| 47. |

| ...or to flattened crop, and finish the reconstruction of the 2011 Temple Farm formation.
|
|
| 48. |


| The final result, matched with two aerial images.
|






















































