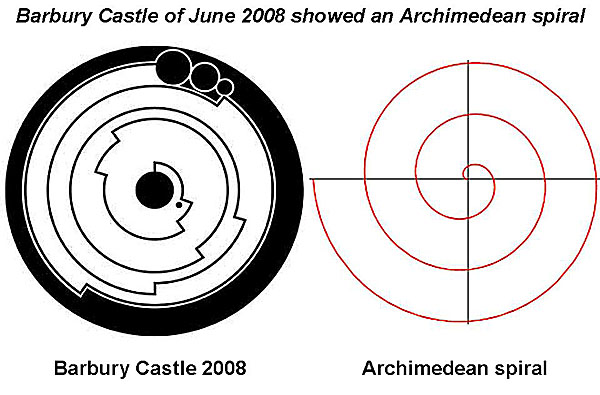
Barbury Castle of June 1, 2008 showed the first ten digits of pi = 3.141592654 in a very clever form, which took everyone in the whole world almost one week to figure out. The puzzle was finally solved by Mike Reed in North Carolina, while Michael Glickman from England came a close second (see Easy-pi-Astrophysicist-solves-riddle-Britains-complex-crop-circle  or temporarytemples.blogware.com blog).   To summarize briefly, that amazing crop picture showed series of ten digits such as “3”, “1” or “4” in the form of an arithmetic or Archimedean spiral: Each digit n rotated around the spiral by n x 36o, say by 3 x 36o = 108o for digit “3”. Then there was a ratchet-step drawn to separate digit “3” from digit “1”, as well as a “decimal point”, and so on.    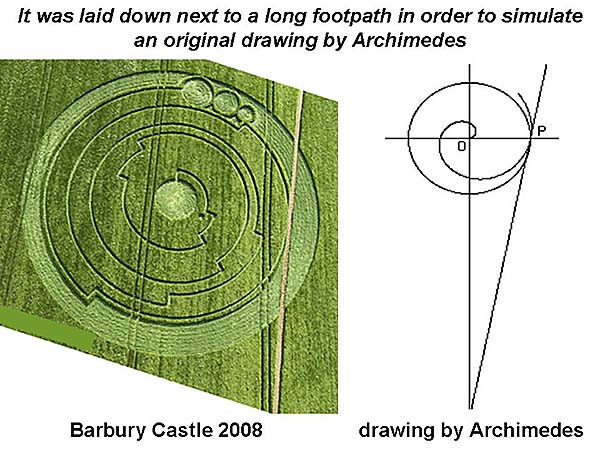The Archimedean spiral and a nearby footpath  Why do we call it an Archimedean spiral? Well, Archimedes of Syracuse once used that particular kind of spiral in 250 BC, in order to find a square and circle of equal areas (see On_Spirals). 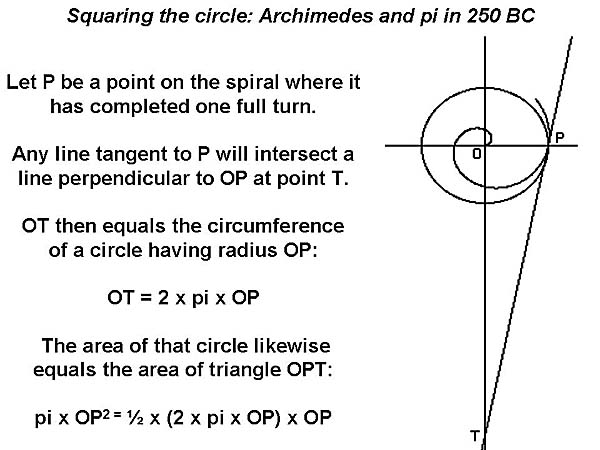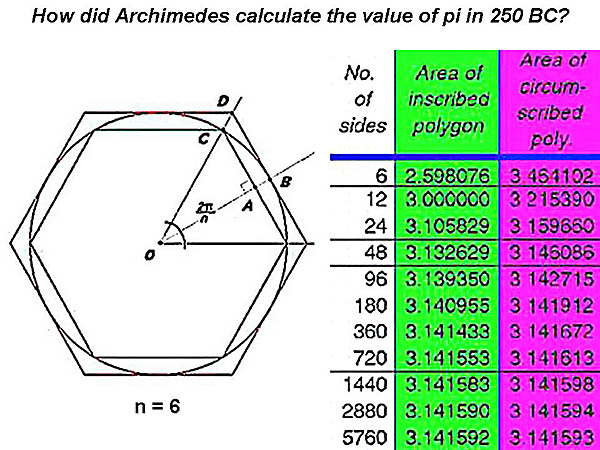Indeed, the entire Barbury crop picture was laid down next to a long footpath, apparently so that it would resemble a drawing by Archimedes on the same subject (see Squaring_the_circle):  Some of his original derivation is shown below:  Calculating pi by polygons   Now Archimedes was also a great innovator when it came to calculating pi: "He realized that the value of pi could be estimated by drawing two regular polygons inside or outside of a circle, and calculating the area of each" (see wikipedia.org/wiki/Pi):     How did Archimedes arrive at such a clever calculation, 2250 years ago before the invention of modern calculators? Simply by thinking! Thus for a regular polygon of n sides, where n = even, the area of his inner polygon = n x sin (360o / 2n) x cos (360o / 2n), while the area of his outer polygon = n x tan (360o / 2n). For example when n = 6, the area of his inner polygon = 6 x 2 x 1 / 2 x sin (30o) x cos (30o) = 2.598076, while the area of his outer polygon = 6 x 2 x 1 / 2 x tan (30o) = 3.464102. The true value of pi as 3.141593 lies roughly halfway between.   Another way to do the same calculation might be to measure perimeters rather than areas. His two formulae then become: inner perimeter = n x 2 x sin (360o / 2n) and outer perimeter = n x 2 x tan (360o / 2n). Yet the results remain almost the same.   Using high precision numbers (see alimentarus.net), I repeated the classical calculation of Archimedes for much larger values of n, in order to ask how large a value might be necessary to reach the ten-digit accuracy of 3.141592654 as shown at Barbury Castle? (see barburyRC2008)  Table 1. Calculation of pi to an accuracy of 3.141592654 requires more than                n = 100,000 but less than n = 1,000,000 polygonic sides   number of sides n 360o / 2n n x sin (360o / 2n) x cos (360o / 2n) n x tan (360o / 2n) actual value of pi 100 1.8o 3.1395 3.1426 3.1416 1000 0.18o 3.141572 3.141603 3.141593 10,000 0.018o 3.14159245 3.14159276 3.14159265 100,000 0.0018o 3.1415926515 3.1415926546 3.1415926536 1,000,000 0.00018o 3.14159265357 3.14159265360 3.14159265359 The answer seems to be more than n = 100,000, but somewhat less than n = 1,000,000 polygonic sides. If we next let n symbolize "days" (a common kind of double meaning in modern crop pictures), then n = 100,000 gives 274 years, while n = 1,000,000 gives 2740 years.  Now Archimedes lived 2250 years (or 800,000 days) ago in ancient Syracuse. A pretty good match! By showing us an Archimedean spiral with a finite value of pi, laid down next to a long footpath, were those crop artists trying to date his classical calculation of pi to a certain time in our distant past?   Charles Reed (with thanks to Mike Reed for comments)   Appendix. His planetarium and the Antikythera device. Three large “balls” shown at the top of Barbury Castle (see above) were probably meant to represent the planets Earth, Venus and Mars. Nearly identical symbols were shown at Secklendorf in Germany only weeks later (see Secklendorf). Why would those crop artists add three planets to an Archimedean spiral representing pi? Perhaps because Archimedes was a great astronomer as well as a great mathematician!  Indeed, after he died in the siege of Syracuse, the conquering general Marcellus carried a planetarium that Archimedes had made back to Rome with him. It showed planetary orbits for Venus, Mars, Jupiter and Saturn as seen from Earth (see brunelleschi.imss.fi.it). There is some reason to believe that Archimedes may have also helped to build the Antikythera device, an early astronomical computer found in a shipwreck off Greece (see www.newscientist.com).