2003 Weyhill formation




|
Reconstruction of the 2003 Weyhill formation | ||
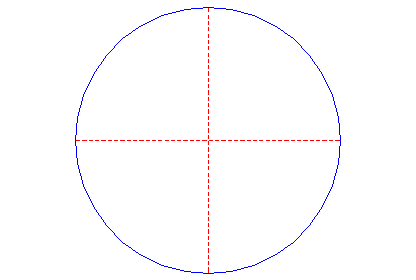
| 1. | 
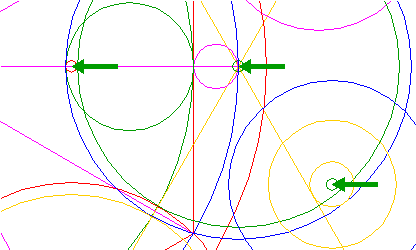
| Draw a circle. Draw the horizontal and vertical centerlines. |
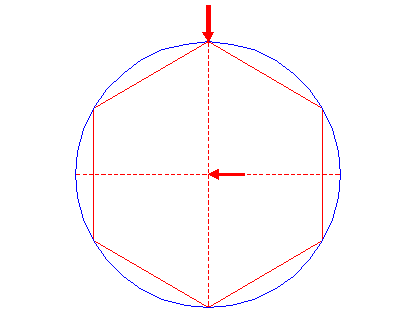
| 2. | 
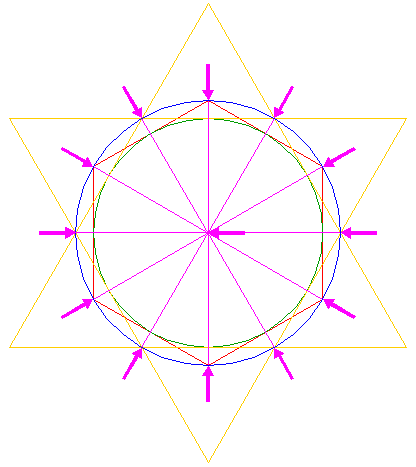
| Construct the inscribed hexagon (regular 6-sided polygon) of circle 1, pointing up. |
| 3. | 
| Construct the inscribed circle of hexagon 2. |
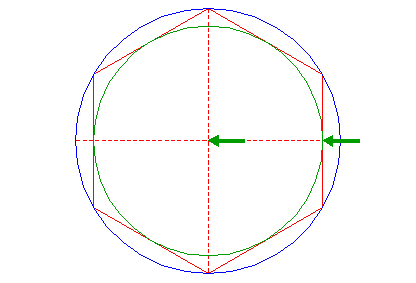
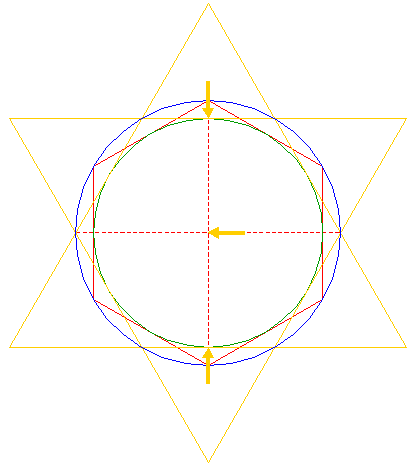
| 4. | 
| Create the circumscribed hexagram (regular 6-pointed star) of circle 3, by constructing two circumscribed equilateral triangles, one pointing up, one pointing down. |
| 5. | 
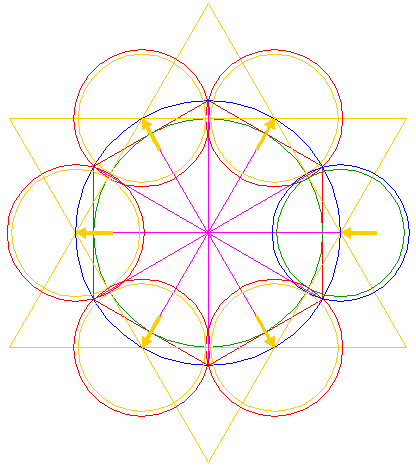
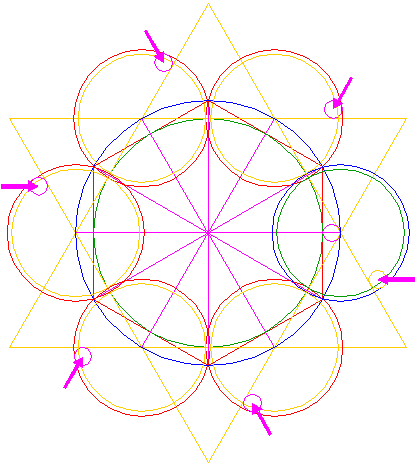
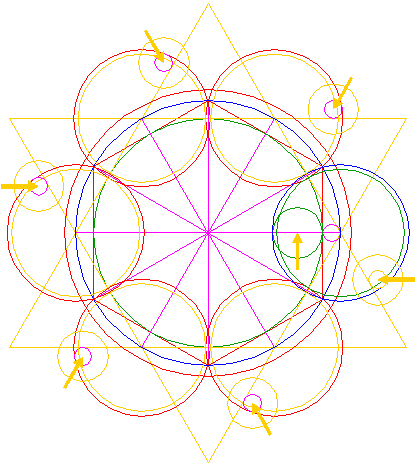
| Draw twelve rays from the center of circle 1, six to the angular points of hexagon 2 and six to the mutual intersections of the two triangles making up hexagram 4, as shown. |
| 6. | 
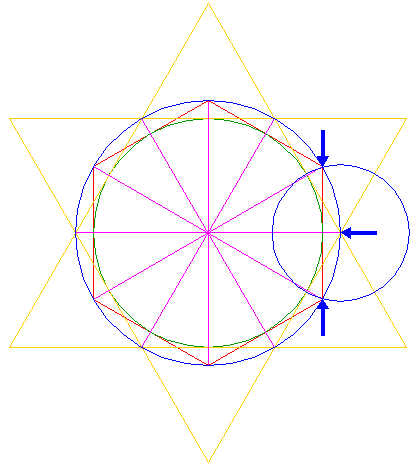
| Construct a circle centered at the right intersection of triangles 4, passing through the end-points of the right side of hexagon 2. |
| 7. | 
| Copy circle 6 five times, to the remaining intersections of triangles 4. |
| 8. | 
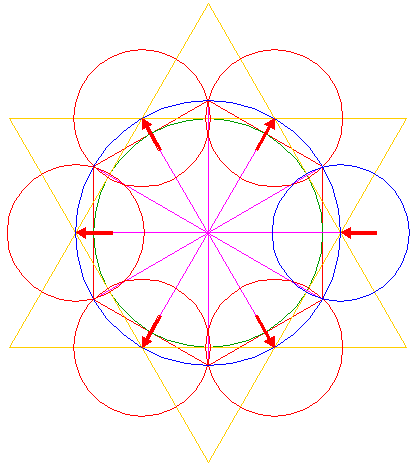
| Construct a circle concentric to circle 6, tangent to the adjacent circles 7 at the near sides, as shown. |
| 9. | 
| Copy circle 8 five times, to the centers of circles 7. |
| 10. | 
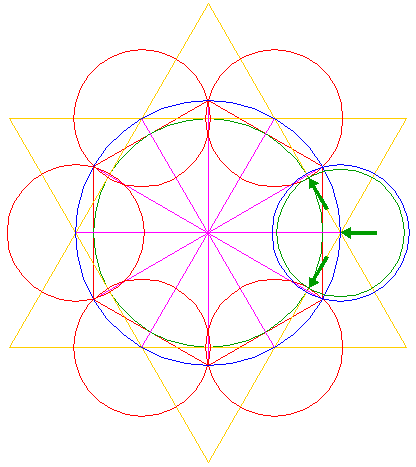
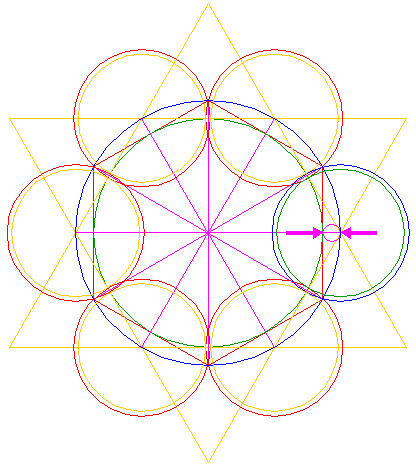
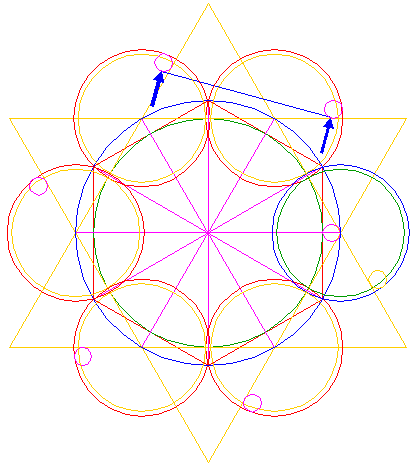
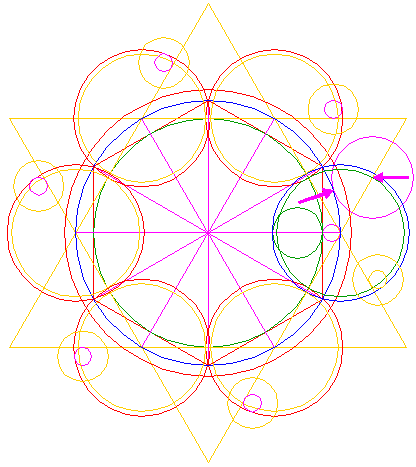
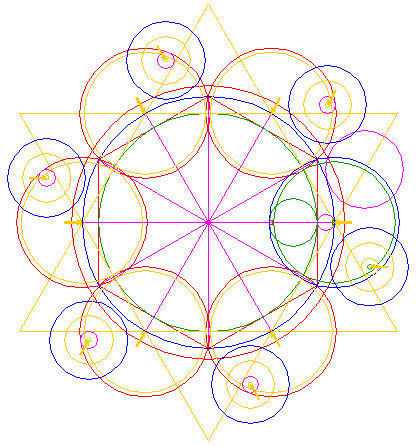
| Construct a circle with a centerline the end-points of which coincide with the intersections of the right horizontal ray 5 and circles 1 and 3 respectively. |
| 11. | 
| Copy circle 10 to the lower intersection of circle 6 and the right side of triangle 4 pointing up. |
| 12. | 
| Construct a circle concentric to circle 6, tangent to circle 11 at the near side. |
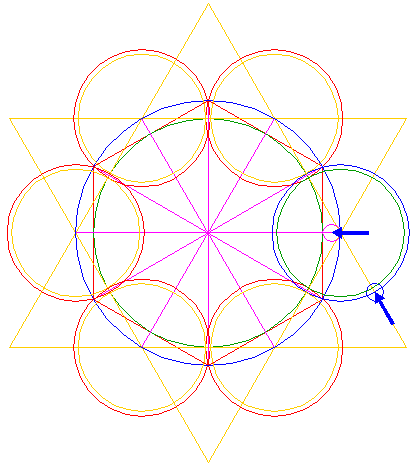
| 13. | 
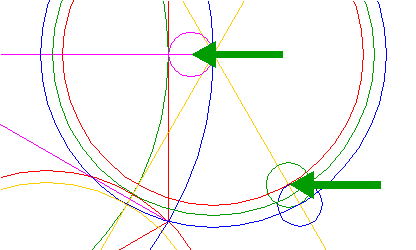
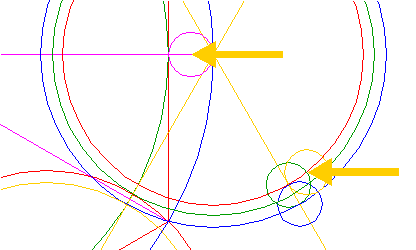
| Copy circle 10 to the lower intersection of circle 12 and the right side of triangle 4 pointing up, see detail. |

| ||
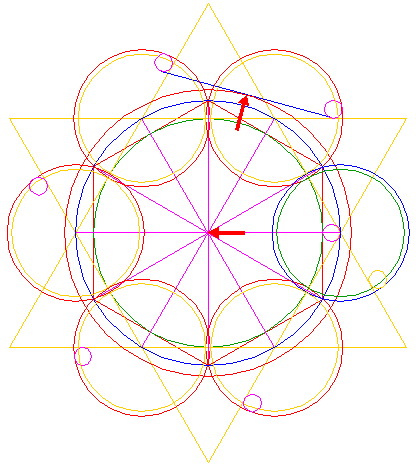
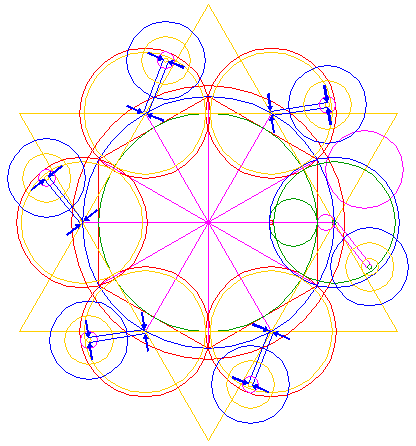
| 14. | 
| Copy circle 10 to the right intersection of circles 12 and 13, see detail. This circle is tangent both to one side of one triangle 4 and to circle 6. |

| ||
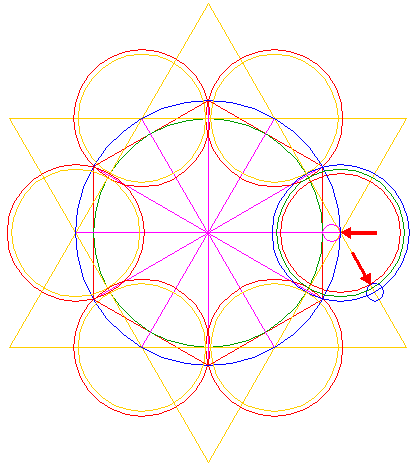
| 15. | 
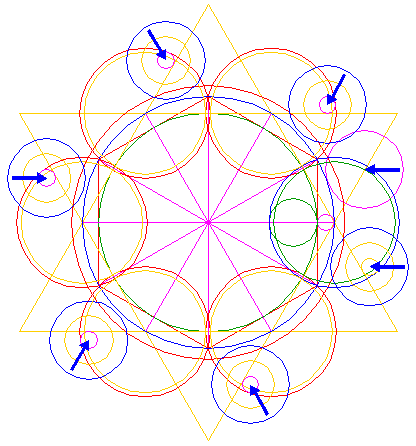
| Copy circle 14 (10) five times, to the corresponding positions with respect to the remaining sides of triangles 4 and circles 7, as shown. |
| 16. | 
| Construct a line, tangent to the two upper circles 15 at the lower sides. |
| 17. | 
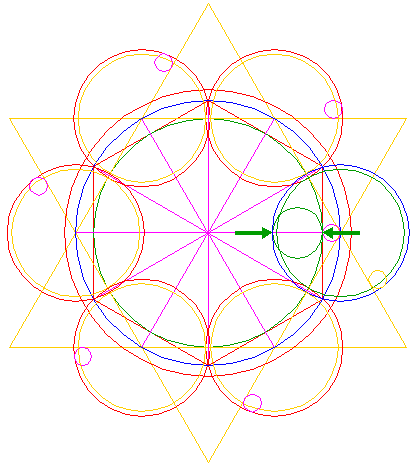
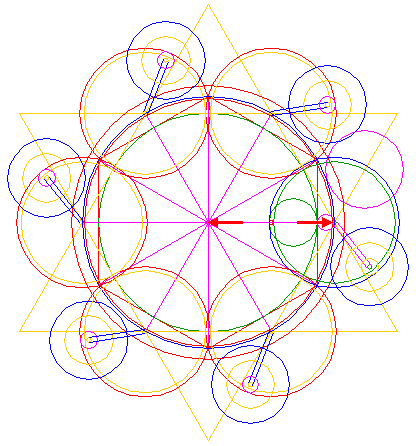
| Construct a circle concentric to circle 1, tangent to line 16. |
| 18. | 
| Construct a circle with a centerline the end-points of which coincide with the intersections of the right horizontal ray 5 and circles 3 and 6 respectively. |
| 19. | 
| Copy circle 18 six times, to the centers of circles 14 and 15. |
| 20. | 
| Construct a circle centered at the upper intersection of circle 8 and the right side of triangle 4 pointing down, tangent to circle 1 at the near side, as shown. |
| 21. | 
| Copy circle 20 six times, to the centers of circles 19. |
| 22. | 
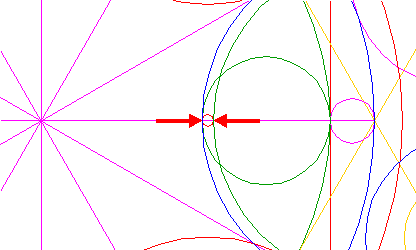
| Construct a small circle with a centerline the end-points of which coincide with the intersections of the right horizontal ray 5 and circles 6 and 8 respectively. |
| 23. | 
| Copy circle 22 two times, to the center of circle 14 and to the right intersection of triangles 4, as shown. |
| 24. | 
| Construct two parallel lines, tangent at both sides to circles 23, as shown. |
| 25. | 
| Copy the two circles 23 five times, to the centers of circles 15 and the remaining intersections of triangles 4. |
| 26. | 
| Repeat step 24 for the corresponding sets of circles 25. |
| 27. | 
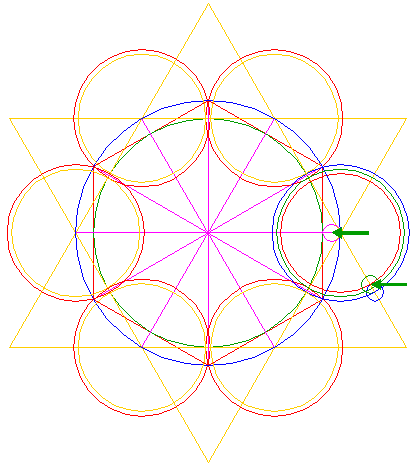
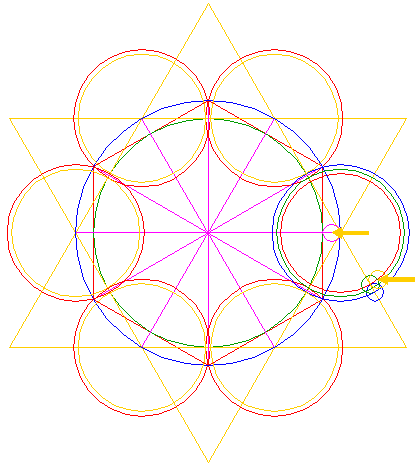
| Construct a circle concentric to circle 1, tangent to the left circle 23 at the left side, see detail. |

| ||
| 28. | 
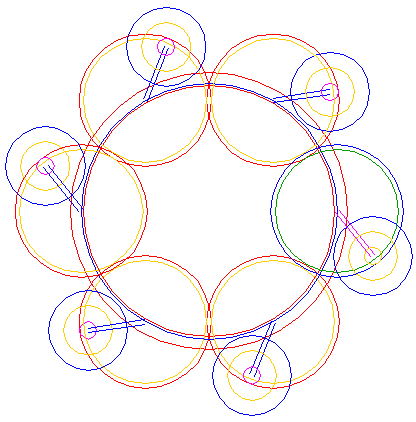
| Circles 1, 6, 7, 8, 9, 14, 15, 17, 19, 21, and 27, and lines 24 and 26 make up the necessary ingredients for the reconstruction. |
| 29. | 
| Leave out all parts not visible in the formation. |
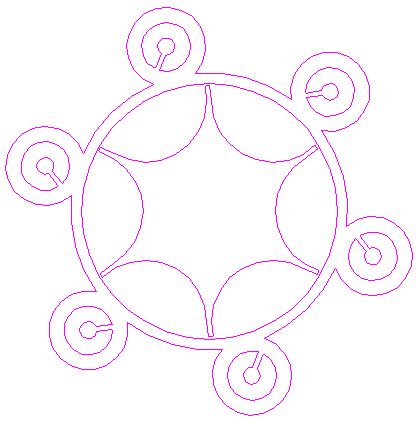
| 30. | 
| Finish the reconstruction of the 2003 Weyhill formation, by colouring the areas corresponding to standing... |
| 31. | 
| ...or to flattened crop. |
| 32. | 
| The final result, matched with the aerial image. At some positions, the reconstruction does not fit. |
| Copyright © 2003, Zef Damen, The Netherlands |