2001 Berranburgh Field formation
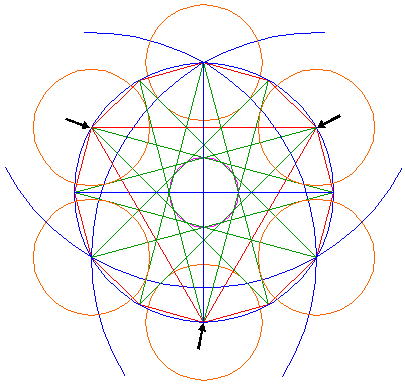
Now, all ingredients are there.

|
Reconstruction of the 2001 Berranburgh Field formation | ||
| 1. |  |
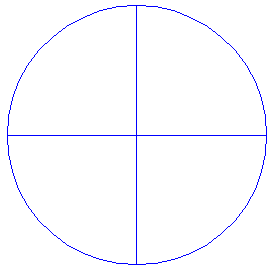
Draw a circle. Draw the horizontal and vertical centerlines. |
| 2. |  |
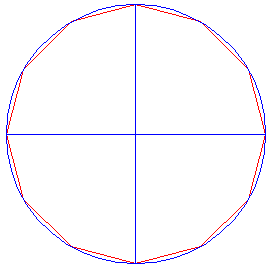
Construct a regular 12-sided polygon (a dodecagon), inscribed in this circle, with angular points at the ends of the centerlines. |
| 3. |  |
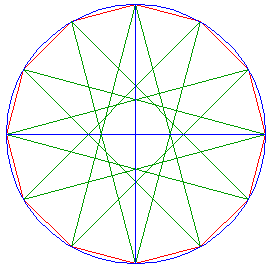
Draw the diagonals between angular points five apart, resulting in a twelve-pointed star. |
| 4. |  |
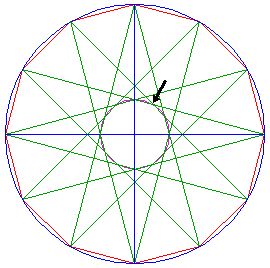
Construct a circle concentric with the larger one, with a radius up to the intersection of two neighbouring diagonals, as shown. |
| 5. |  |
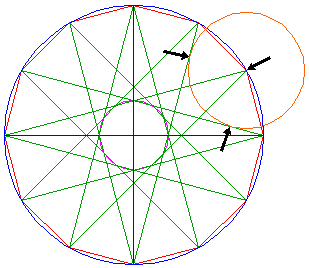
Construct a circle with its center at an angular point of the twelve-pointed star, tangent to two adjacent diagonals (intersecting each other perpendicularly), as shown. |
| 6. |  |
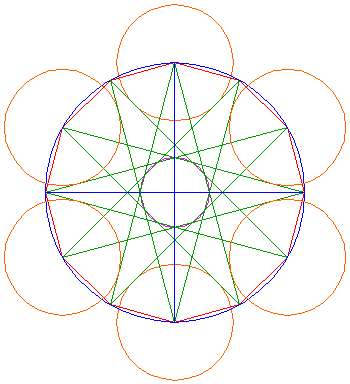
Repeat this another five times, up to a total of six circles, evenly distributed over the points of the twelve-pointed star. |
| 7. |  |
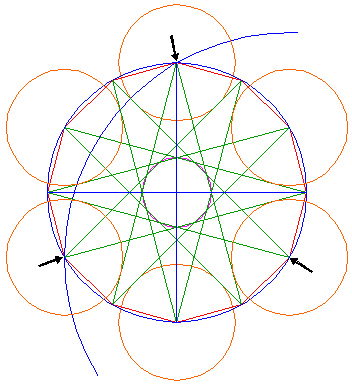
Draw a circle concentric with one of the circles 6, and passing through two points of the twelve-pointed star, that are four apart from the one in the center, see figure. |
| 8. |  |
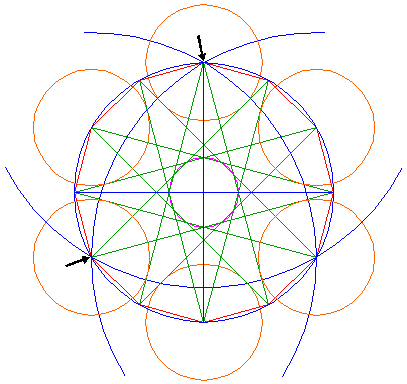
Repeat this for the other two points just passed. |
| 9. |  |
Construct an equilateral triangle from the three points of the twelve-pointed star half way in between the previous points, as shown. Now, all ingredients are there. |
| 10. |  |
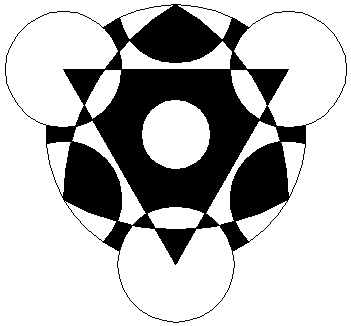
Removing all superfluous parts results in the reconstruction of the 2001 Berranburgh Field formation. (Black denotes standing crop). |
| 11. |  |
The final result, matched with the aerial image. |
| Copyright © 2001, Zef Damen, The Netherlands |