Reconstruction Woodborough Hill (3) 2000

Reconstruction of the 2000 Woodborough Hill (3) formation

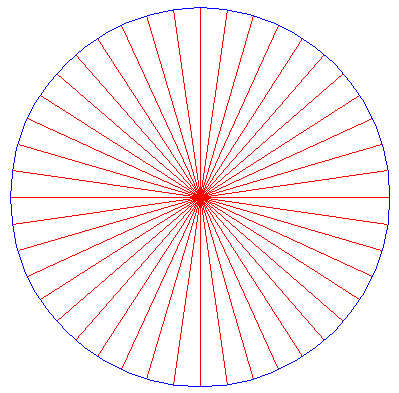
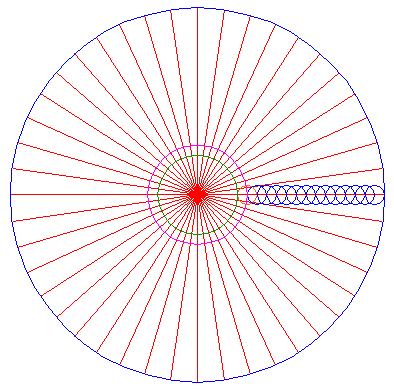
1.		Draw a circle.

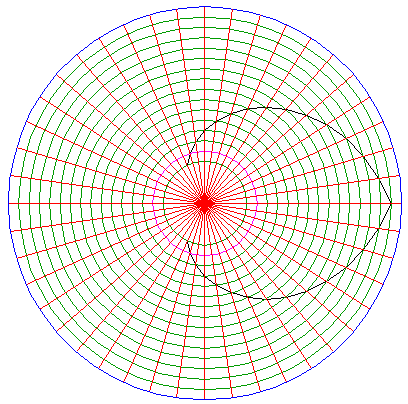
2.		Divide the circumference into 44 equal parts and draw the rays. (Notice that this necessitates the construction of a regular 11-fold polygon, which can not be done exactly by the "ruler-and-compass" construction method (this applies equally to 7, 9, 13, 14, 18, 19...-fold polygons). See for instance Eric Weisstein's excellent World of Mathematics for constructible polygons).

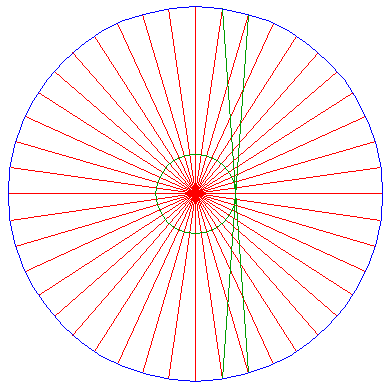
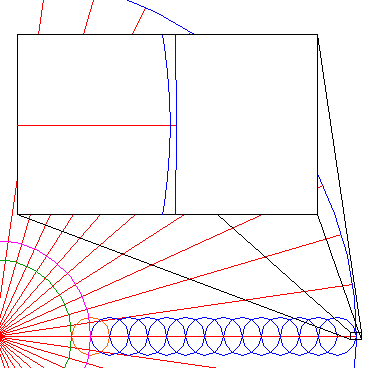
3.		Draw the two diagonals as shown in the figure. Construct a circle centered at the center of the pattern, passing through the intersection of the two diagonals.

4.		Draw two other diagonals as shown, and construct again a circle passing through the intersection.

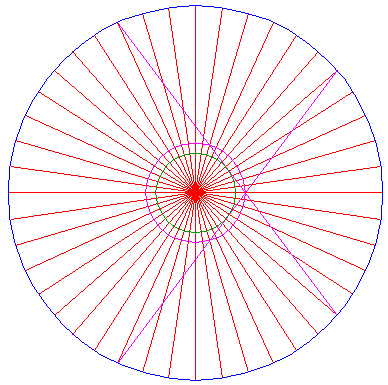
5.		Construct a small circle, centered at the intersection of the second circle and the horizontal centerline, with a radius equal to the distance between the two circles (of the previous steps).

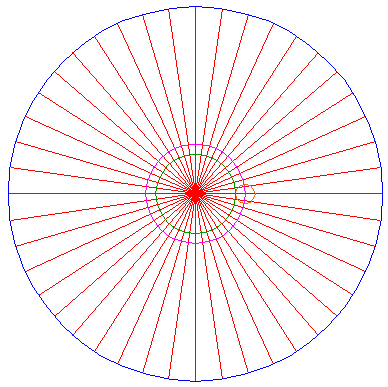
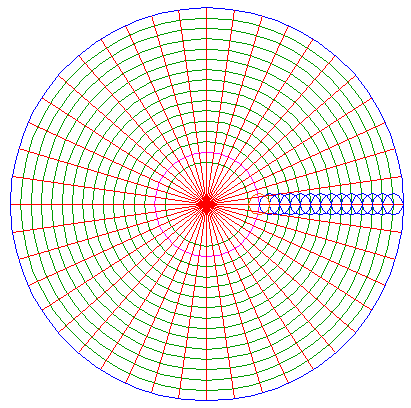
6.		This small circle is used to "distribute" this distance along the horizontal centerline. Therefore, construct a series of small circles, centered at every next intersection with the horizontal centerline, each with the same radius as the first one, thirteen in total.

6a.		Accurate measurement reveals the remarkable fact, that the last small circle almost exactly touches the outer circle. The difference (enlarged here) only amounts to 0,0006114114... times the radius of the outer circle, or 1 into 1635,56! Therefore, the series divides the distance between the smaller central circle and the outer circle (almost exactly) into 15 equal parts.

7.		Construct 13 concentric circles passing through the intersections of the series of small circles and the horizontal centerline.

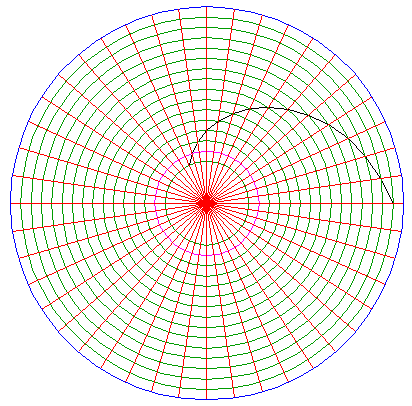
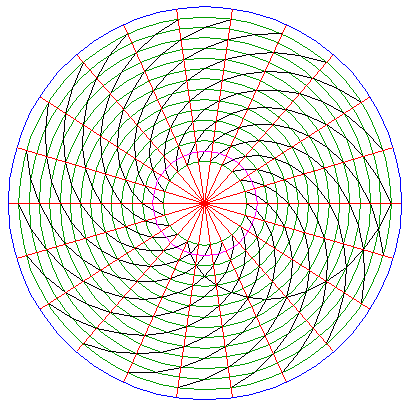
8.		Starting from the intersection of the second last central circle and the horizontal centerline, draw a line to the intersection of the next ray (up) and the previous central circle. Repeat this until the smallest central circle is reached. (These lines essentially form a *spiral*, obeying the rule of a "travelling" point the distance of which to the origin is linear proportional to the angle it makes with the horizontal, r = a θ).

9.		Repeat the same construction in the other direction, down in stead of up.

10.		Repeat the construction of the upper spiral another 21 times (22 in total), evenly distributed around the circle.

11.		And do this also for the lower spiral.

12.		Making black every other "triangle" (one of the sides is circular!) in a checkerboard-like fashion reveals the reconstruction of the 2000 Woodborough Hill (3) formation (black represents standing crop). The pattern resembles very much the positioning of seeds in for instance sunflowers or the scales in a pinecone; a very good site dealing with this matter can be found at R. Knott's personal pages.

13.		The final result, matched with the aerial image.

Hit Counter