Reconstruction Bishop Cannings 2000

Reconstruction of the 2000 Bishop Cannings formation

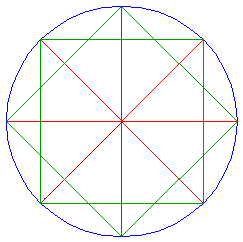
1.		Draw a circle (the inner side of the ring).

2.		Draw centerlines at 45°.

3.		Construct two squares, one horizontal, one diagonal.

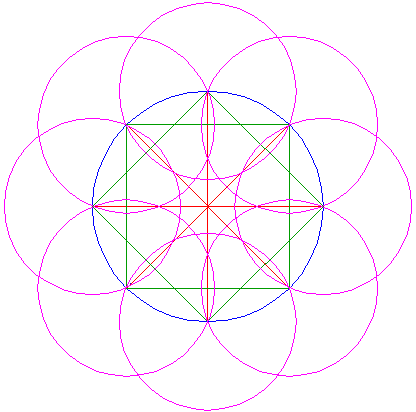
4.		Draw eight circles, centered at the corners of the squares, and passing through the adjacent corners.

5.		To determine the outer boundary of the ring, construct two larger squares through the corners of the smaller ones (of step 3), as shown.

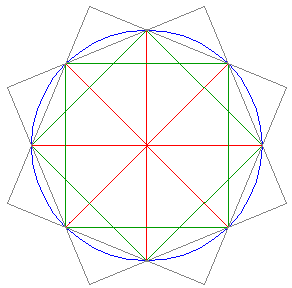
6.		Construct a large octagon (a regular eight-fold polygon) by connecting the corners of the larger squares.

7.		Extend the four centerlines up to the sides of the large octagon.

8.		From the endpoints of the centerlines, construct again an octagon, inscribed in the large one.

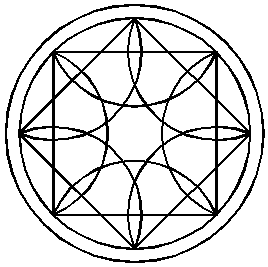
9.		The outer border of the ring is formed by a circle, inscribed in the octagon of the previous step.

10.		Removing all superfluous parts will yield the reconstruction of the 2000 Bishop Cannings formation.

11.		The final result, matched with the aerial image.

Hit Counter